What Is Rolles Theorem And Mean Value Theorem

Rolle S Theorem Lagrange S Mean Value Theorem And Examples The mean value theorem is one of the most important theorems in calculus. we look at some of its implications at the end of this section. first, let’s start with a special case of the mean value theorem, called rolle’s theorem. Rolle's theorem and the mean value theorem are fundamental results in differential calculus that provide crucial insights into the behavior of differentiable functions.
Difference Between Rolle S Theorem And Mean Value Theorem Homework This version of rolle's theorem is used to prove the mean value theorem, of which rolle's theorem is indeed a special case. it is also the basis for the proof of taylor's theorem. although the theorem is named after michel rolle, rolle's 1691 proof covered only the case of polynomial functions. Rolle’s theorem is a special case of the mean value theorem. it states that for any continuous, differentiable function with two equal values at two distinct points, the function must have a point where the first derivative is zero. They are critical points, rolle's theorem and the mean value theorem. the rst thing to think about is when a function might have a high or low place. this means that, at least locally, there is value for the function which is the highest one around or the lowest one around. The rolle's theorem: assume f is a function that is continuous on [a; b], di erentiable on (a; b) and f(a) = f(b), then there is a number c in (a; b) such that f0(c) = 0:.

Rolle S Theorem And The Mean Value Theorem Rivisiontown They are critical points, rolle's theorem and the mean value theorem. the rst thing to think about is when a function might have a high or low place. this means that, at least locally, there is value for the function which is the highest one around or the lowest one around. The rolle's theorem: assume f is a function that is continuous on [a; b], di erentiable on (a; b) and f(a) = f(b), then there is a number c in (a; b) such that f0(c) = 0:. In this lecture, we look at the mean value theorem and a special case called rolle's theorem. unlike the intermediate value theorem which applied for continuous functions, the mean value theorem involves derivatives. Both rolle's and the mean value theorem are statements of pure existence. except for claiming that point c lies in the interval (a, b), neither provides more accurate information as to its location. In general, one can understand mean as the average of the given values. but in the case of integrals, the process of finding the mean value of two different functions is different. let us learn rolle’s theorem and the mean value of such functions and their geometrical interpretation. The mean value theorem for derivatives is a little bit more important and is proven using the rolle’s theorem. it says that somewhere inside a closed interval $ [a,b]$ there exists a point $ c$ where the derivative at this point is the same as the slope between points $ a$ and $ b$.

Rolle S Theorem Mean Value Theorem In this lecture, we look at the mean value theorem and a special case called rolle's theorem. unlike the intermediate value theorem which applied for continuous functions, the mean value theorem involves derivatives. Both rolle's and the mean value theorem are statements of pure existence. except for claiming that point c lies in the interval (a, b), neither provides more accurate information as to its location. In general, one can understand mean as the average of the given values. but in the case of integrals, the process of finding the mean value of two different functions is different. let us learn rolle’s theorem and the mean value of such functions and their geometrical interpretation. The mean value theorem for derivatives is a little bit more important and is proven using the rolle’s theorem. it says that somewhere inside a closed interval $ [a,b]$ there exists a point $ c$ where the derivative at this point is the same as the slope between points $ a$ and $ b$.
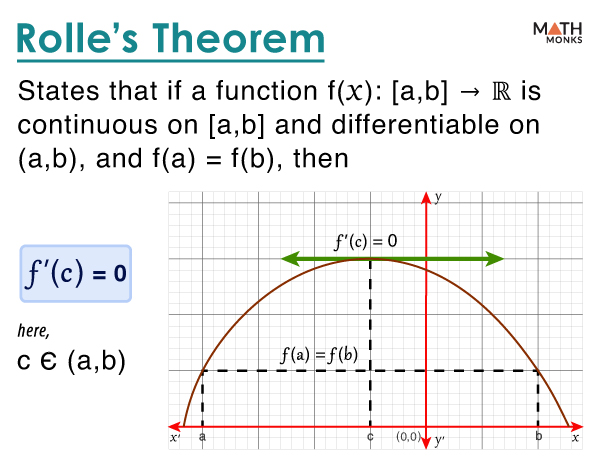
Rolle S Theorem Conditions Formula Proof And Examples In general, one can understand mean as the average of the given values. but in the case of integrals, the process of finding the mean value of two different functions is different. let us learn rolle’s theorem and the mean value of such functions and their geometrical interpretation. The mean value theorem for derivatives is a little bit more important and is proven using the rolle’s theorem. it says that somewhere inside a closed interval $ [a,b]$ there exists a point $ c$ where the derivative at this point is the same as the slope between points $ a$ and $ b$.
Comments are closed.