What Is Empty Setempty Set Definitionhouse Of Mathematics

The Empty Set в Symbol In Mathematics The empty set plays a vital role in defining various mathematical structures, such as groups, rings, and topological spaces. it is also used extensively in abstract algebra, topology, category theory, and type theory. A set that does not contain any element is called an empty set or a null set. an empty set is denoted using the symbol '∅'. it is read as 'phi'. example: set x = {}. it is also called a void set or null set. empty sets are considered to be unique when compared to other sets.
Empty Set Explanation Examples Intuitively, the empty set contains nothing. the set containing only the empty set is a set maden of one element, which in this case is the empty set. hence it contains something, is just a set maden by another set. The empty set is defined as a set containing no elements. it is denoted by the symbol ∅ or empty curly braces { }. this concept is simple, yet it plays a crucial role in mathematics. the empty set is unique as it is the only set with a cardinality of zero, which means it contains no elements at all. What is an empty set? the concept of an empty set is fundamental in the field of mathematics, particularly in set theory. an empty set, often denoted by the symbol ∅ or { }, is a set that contains no elements. this means that there are no members or objects within the set, making it unique in its definition. In mathematics, a set is a collection of different things; the things are elements or members of the set and are typically mathematical objects: numbers, symbols, points in space, lines, other geometric shapes, variables, or other sets.
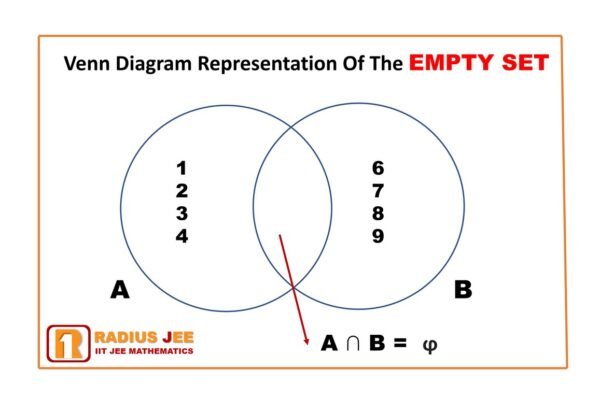
Definition Of Empty Set In Mathematics Radius Jee What is an empty set? the concept of an empty set is fundamental in the field of mathematics, particularly in set theory. an empty set, often denoted by the symbol ∅ or { }, is a set that contains no elements. this means that there are no members or objects within the set, making it unique in its definition. In mathematics, a set is a collection of different things; the things are elements or members of the set and are typically mathematical objects: numbers, symbols, points in space, lines, other geometric shapes, variables, or other sets. What is an empty set? an empty set is a special set in mathematics that contains no elements at all. it is also called a null set or void set. the concept is simple but powerful: whenever a set is defined in such a way that nothing fits its rule or condition, it becomes an empty set. The empty set is a set which has no elements. that is, $x \in \o$ is false, whatever $x$ is. it is usually denoted by some variant of a zero with a line through it, for example $\o$ or $\emptyset$, and can always be represented as $\set {}$. the concept of the empty set is axiomatised in the axiom of the empty set in zermelo fraenkel set theory:. In any model of our axioms, an element m' ∈ m will satisfy the open formula “∀ y y ∉ x ” if and only if the set {m | m ⊨ m ∈ m' } is really empty. hence, there's at least a sense in which we can still capture the notion “ x is the empty set” from within the algebraic framework. But in non natural set theory, there only is one ‘empty set’; in the theory, you cannot have a set whose elements are three ‘empty sets’.

Empty Set Definition Notation Example And Properties Of Empty Set What is an empty set? an empty set is a special set in mathematics that contains no elements at all. it is also called a null set or void set. the concept is simple but powerful: whenever a set is defined in such a way that nothing fits its rule or condition, it becomes an empty set. The empty set is a set which has no elements. that is, $x \in \o$ is false, whatever $x$ is. it is usually denoted by some variant of a zero with a line through it, for example $\o$ or $\emptyset$, and can always be represented as $\set {}$. the concept of the empty set is axiomatised in the axiom of the empty set in zermelo fraenkel set theory:. In any model of our axioms, an element m' ∈ m will satisfy the open formula “∀ y y ∉ x ” if and only if the set {m | m ⊨ m ∈ m' } is really empty. hence, there's at least a sense in which we can still capture the notion “ x is the empty set” from within the algebraic framework. But in non natural set theory, there only is one ‘empty set’; in the theory, you cannot have a set whose elements are three ‘empty sets’.

Set Pdf Empty Set Set Mathematics In any model of our axioms, an element m' ∈ m will satisfy the open formula “∀ y y ∉ x ” if and only if the set {m | m ⊨ m ∈ m' } is really empty. hence, there's at least a sense in which we can still capture the notion “ x is the empty set” from within the algebraic framework. But in non natural set theory, there only is one ‘empty set’; in the theory, you cannot have a set whose elements are three ‘empty sets’.

Set Lp 114719 Pdf Empty Set Mathematical Concepts
Comments are closed.