What Are Common Euclidean Geometry Problems Science Through Time

Problems And Solutions In Euclidean Geometry Pdf Triangle Line What are common euclidean geometry problems? in this engaging video, we will explore the fascinating world of euclidean geometry and the common problems that arise within this. Explore the ancient roots, challenges, and practical applications of euclidean geometry in this insightful overview of its enduring impact on mathematics.

Euclideangeometryquestionsandsolutions Final Pdf The origins of euclidean geometry geometry before euclid geometry, the study of shapes, sizes, and the properties of space, predates euclid by centuries. ancient civilizations, including the egyptians and babylonians, used geometric principles for practical purposes such as land measurement, construction, and astronomy. Welcome to a detailed exploration of euclidean geometry, a foundational branch of mathematics that has shaped our understanding of space and shapes for centuries. this guide will delve into the core concepts, axioms, and theorems that define euclidean geometry, providing a clear and accessible overview for students and enthusiasts alike. we’ll cover the basics, from points and lines to more. Euclidean geometry is the study of plane and solid figures on the basis of axioms and theorems employed by the ancient greek mathematician euclid. the term refers to the plane and solid geometry commonly taught in secondary school. euclidean geometry is the most typical expression of general mathematical thinking. Euclidean geometry is the study of 2 dimensional geometrical shapes and figures. euclidean geometry is based on different axioms and theorems. the word geometry is derived from the greek words ‘geo’ meaning earth and ‘metrein’ meaning ‘to measure’. thus, geometry is the measure of the earth or various shapes present on the earth. euclidean geometry as the name suggests was first.

Euclidean Geometry Theorems With Reasons Pdf Circle Triangle Euclidean geometry is the study of plane and solid figures on the basis of axioms and theorems employed by the ancient greek mathematician euclid. the term refers to the plane and solid geometry commonly taught in secondary school. euclidean geometry is the most typical expression of general mathematical thinking. Euclidean geometry is the study of 2 dimensional geometrical shapes and figures. euclidean geometry is based on different axioms and theorems. the word geometry is derived from the greek words ‘geo’ meaning earth and ‘metrein’ meaning ‘to measure’. thus, geometry is the measure of the earth or various shapes present on the earth. euclidean geometry as the name suggests was first. Explore five mathematical problems that changed history, from pythagoras to fermat’s last theorem, shaping science, and innovation. The purpose of this note is to describe several challenging problems in euclidean geometry. the note also contains author’s solution sketches to the two problems. Euclidean geometry is a mathematical system that assumes a small set of axioms and deductive propositions and theorems that can be used to make accurate measurement of unknown values based on their geometric relation to known measures. An important open problem in combinatorial euclidean geometry is the question of how many different halving lines a set of $2n$ points in the euclidean plane may have, in the worst case.

Euclidean Geometry Free Maths And Science Lessons Explore five mathematical problems that changed history, from pythagoras to fermat’s last theorem, shaping science, and innovation. The purpose of this note is to describe several challenging problems in euclidean geometry. the note also contains author’s solution sketches to the two problems. Euclidean geometry is a mathematical system that assumes a small set of axioms and deductive propositions and theorems that can be used to make accurate measurement of unknown values based on their geometric relation to known measures. An important open problem in combinatorial euclidean geometry is the question of how many different halving lines a set of $2n$ points in the euclidean plane may have, in the worst case.
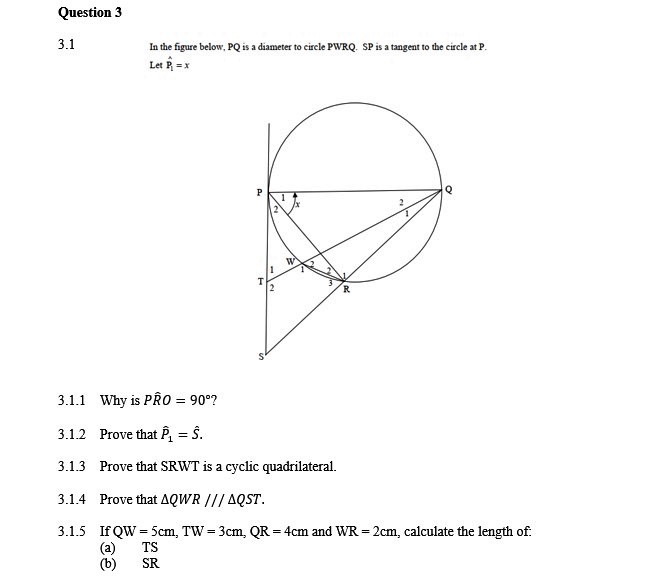
Jenn Mathematics Euclidean Geometry Euclidean geometry is a mathematical system that assumes a small set of axioms and deductive propositions and theorems that can be used to make accurate measurement of unknown values based on their geometric relation to known measures. An important open problem in combinatorial euclidean geometry is the question of how many different halving lines a set of $2n$ points in the euclidean plane may have, in the worst case.
Comments are closed.