What Are Binary And Hexadecimal Number Systems

By healtycares On Aug 24, 2025

Binary And Hexadecimal Number System Pdf Decimal Numbers Binary numbers are just "base 2" instead of "base 10". so we start counting at 0, then 1, then we run out of digits so we start back at 0 again, but increase the number on the left by 1. This comprehensive guide will delve into the binary and hexadecimal number systems, exploring their fundamentals, applications, and importance in coding and computer science.

What Are Binary And Hexadecimal Number Systems Electronic and digital systems use various number systems such as decimal, binary, hexadecimal and octal, which are essential in computing. binary (base 2) is the foundation of digital systems. hexadecimal (base 16) and octal (base 8) are commonly used to simplify the representation of binary data. Binary and hexadecimal are two commonly used number systems in the field of computing. while binary is the most fundamental number system used by computers, hexadecimal is often used as a more human friendly representation of binary data. Learn the most used computer number systems by computer scientists. read on and take a deep dive into binary and hexadecimal conversions. From late latin bīnārius (“consisting of two”). terminology why? 10. 11. 100. 101. 110. 111. 1000. 1001. 1010. 1011. 1100. 1101. 1110. 1111 decimal binary. 10000. 10001. 10010. 10011. 10100. 10101. 10110. 10111. 11000. 11001. 11010. 11011. 11100. 11101. 11110. 11111. why? f decimal hex. 10. 11.

Number Systems Binary Octal Decimal Hexadecimal Learn the most used computer number systems by computer scientists. read on and take a deep dive into binary and hexadecimal conversions. From late latin bīnārius (“consisting of two”). terminology why? 10. 11. 100. 101. 110. 111. 1000. 1001. 1010. 1011. 1100. 1101. 1110. 1111 decimal binary. 10000. 10001. 10010. 10011. 10100. 10101. 10110. 10111. 11000. 11001. 11010. 11011. 11100. 11101. 11110. 11111. why? f decimal hex. 10. 11. Dive into the different number systems used in digital electronics, including binary, decimal, octal, and hexadecimal. learn their applications, conversions, and importance in computing. In the world of computers, there are several number systems, but the three most commonly used are binary, decimal, and hexadecimal. each system serves a unique purpose in digital technologies, with binary being the native language of computers, decimal being the human friendly system, and hexadecimal bridging the gap between the two. Binary and hexadecimal number systems are examples of positional number systems with different bases. binary number systems use a base of two while hexadecimal uses a base of 16. Ented in decimal or other number systems using binary numbers. (1× ) (1× = 8 0 2 1 0 = ) (0× ) (1× ) in general, any number (decimal, binary, octal and hexadecimal) is simply t. e sum of products of each digit value and its positional val.

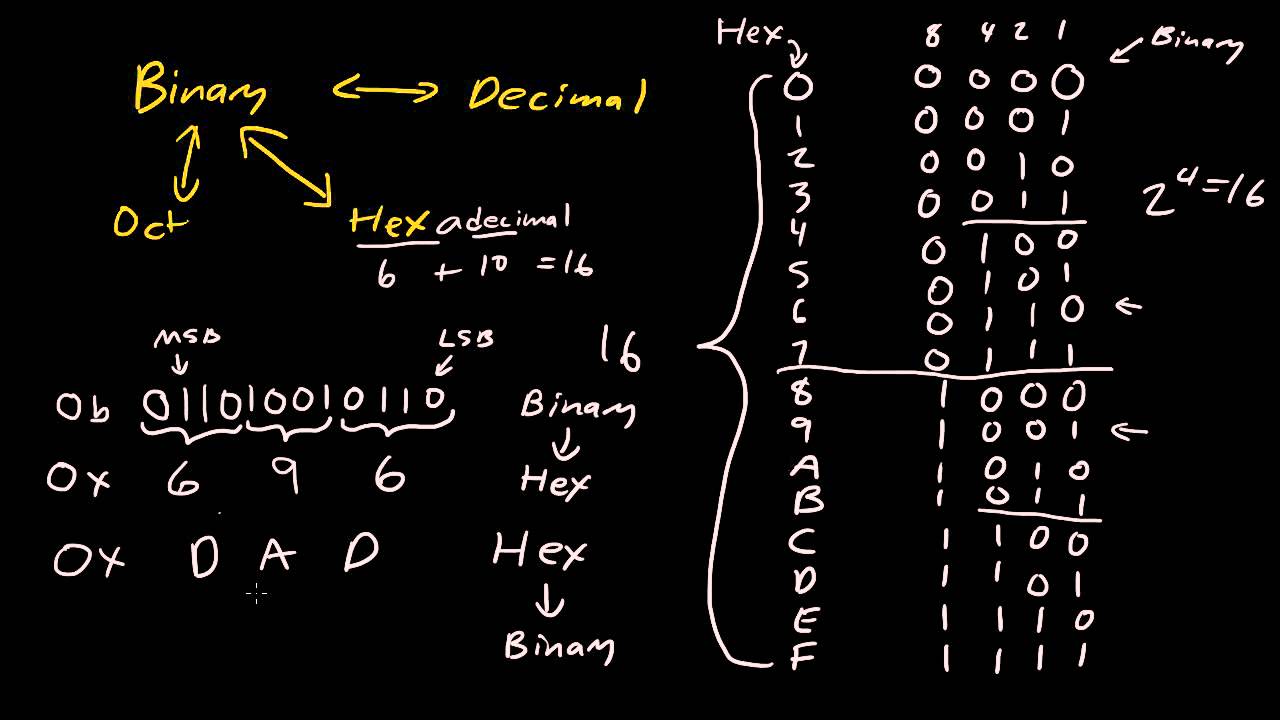
Number Systems Decimal Binary Octal And Hexadecimal Fun Cram Dive into the different number systems used in digital electronics, including binary, decimal, octal, and hexadecimal. learn their applications, conversions, and importance in computing. In the world of computers, there are several number systems, but the three most commonly used are binary, decimal, and hexadecimal. each system serves a unique purpose in digital technologies, with binary being the native language of computers, decimal being the human friendly system, and hexadecimal bridging the gap between the two. Binary and hexadecimal number systems are examples of positional number systems with different bases. binary number systems use a base of two while hexadecimal uses a base of 16. Ented in decimal or other number systems using binary numbers. (1× ) (1× = 8 0 2 1 0 = ) (0× ) (1× ) in general, any number (decimal, binary, octal and hexadecimal) is simply t. e sum of products of each digit value and its positional val.

Unlock the transformative power of What Are Binary And Hexadecimal Number Systems with our thought-provoking articles and expert insights. Our blog serves as a gateway to explore the depths of What Are Binary And Hexadecimal Number Systems, empowering you with the information and inspiration to make informed decisions and embrace the opportunities that What Are Binary And Hexadecimal Number Systems presents. Join us as we navigate the dynamic world of What Are Binary And Hexadecimal Number Systems and unlock its hidden treasures.

Number Systems Introduction - Decimal, Binary, Octal & Hexadecimal

Number Systems Introduction - Decimal, Binary, Octal & Hexadecimal

Number Systems Introduction - Decimal, Binary, Octal & Hexadecimal Understanding Binary, Hexadecimal, Decimal (Base-10), and more Binary Numbers and Base Systems as Fast as Possible How To Convert Binary to Hexadecimal - Computer Science Read and Write in Hexadecimal, The Easy Way! Binary & Hexadecimal Demystified Binary And Hexadecimal Numbering Systems Binary Explained in 01100100 Seconds Hexadecimal to Decimal | Hexadecimal to Binary | Hexadecimal to Octal | Computer Fundamental Why do programmers use hexadecimal numbers? Binary, Decimal and Hexadecimal Number Systems Why Do Computers Use 1s and 0s? Binary and Transistors Explained. Binary and Hexadecimal Systems - Computer Science Number Systems Introduction - Binary, Decimal, Octal and Hexadecimal | PingPoint Hexadecimal number system | Applying mathematical reasoning | Pre-Algebra | Khan Academy Conversions using Binary and Hexadecimal Number Systems Understanding Binary and Hexadecimal Numbers Decimal, Binary and Hexadecimal Number Systems | 9618 | AS Level Computer Science Numbering systems: Decimal, Binary, Hexadecimal

Conclusion

Following an extensive investigation, it is obvious that the write-up gives informative details in connection with What Are Binary And Hexadecimal Number Systems. In every section, the creator displays a deep understanding on the topic. Specifically, the discussion of contributing variables stands out as a significant highlight. The writer carefully articulates how these components connect to develop a robust perspective of What Are Binary And Hexadecimal Number Systems.

Further, the essay is noteworthy in explaining complex concepts in an clear manner. This comprehensibility makes the explanation useful across different knowledge levels. The analyst further enhances the exploration by adding germane illustrations and real-world applications that put into perspective the theoretical constructs.

Another element that sets this article apart is the thorough investigation of several approaches related to What Are Binary And Hexadecimal Number Systems. By exploring these various perspectives, the content gives a impartial picture of the theme. The meticulousness with which the journalist treats the subject is truly commendable and sets a high standard for similar works in this discipline.

To summarize, this write-up not only teaches the audience about What Are Binary And Hexadecimal Number Systems, but also inspires continued study into this intriguing theme. Whether you are a novice or an authority, you will find worthwhile information in this detailed piece. Thank you for this comprehensive post. If you have any inquiries, please do not hesitate to contact me via the comments section below. I am eager to your feedback. To expand your knowledge, you will find various related publications that are potentially interesting and supportive of this topic. Wishing you enjoyable reading!