Week 7 3 5 Variation Of Parameters To Find A Particular Solution 3 6

Solved In Exercises 1 6 Use Variation Of Parameters To Find Chegg Week 7 3 5 variation of parameters to find a particular solution 3 6 cauchy euler differential equations 1) the document discusses variation of parameters, a method to find particular solutions to non homogeneous second order linear differential equations. In this section we will learn the variation of parameters method to solve the non homogeneous equation. as with the method of undetermined coefficients, this procedure relies on knowing solutions to the homogeneous equation.

Solved In Exercises 1 6 Use Variation Of Parameters To Find Chegg In this section we introduce the method of variation of parameters to find particular solutions to nonhomogeneous differential equation. we give a detailed examination of the method as well as derive a formula that can be used to find particular solutions. We vary these two functions in order to get a particular solutionyp. that is because the method is called: the method of variation of parameters. technically, the method of variation of parameters computes the functionsu 1 (x) and u 2 (x). first, place the de instandard form:. In the last section we utilized the method of undetermined coefficients to find a particular solution to a nonhomogeneous linear differential equation. after also solving the associated homogeneous solution we added them together to get the general solution of the linear differential equation. The method of variation of parameters is applicable for any linear de (not only with constant coefficients). however, we have to know a fundamental set of solutions for the associated homogeneous de.

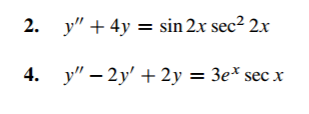
Solved In Exercises 1 6 Use Variation Of Parameters To Find Chegg In the last section we utilized the method of undetermined coefficients to find a particular solution to a nonhomogeneous linear differential equation. after also solving the associated homogeneous solution we added them together to get the general solution of the linear differential equation. The method of variation of parameters is applicable for any linear de (not only with constant coefficients). however, we have to know a fundamental set of solutions for the associated homogeneous de. Once we have found the general solution and all the particular solutions, then the final complete solution is found by adding all the solutions together. this method relies on integration. All terms in the particular solution must be linearly independent of all terms in the homogeneous solution. those that are not may be discarded because they add no useful information. Understand the method of variation of parameters to find a particular solution of second order linear nonhomogeneous differential equations. apply variation of parameters to equations with known solutions of the complementary equation to derive the general solution. Technically, the method of variation of parameters computes the functions u1 (x) and u2 (x). first, place the de in standard form: 00 0 a2 (x)y a1 (x)y a0 (x).