Week 1 Lecture 1 Markov Chains Course

Markov Chains Part 1 Pdf Markov Chain Applied Mathematics Why markov chains? 1.2. random mapping representation. 1.3. irreducibility and aperiodicity. 1.4. random walks on graphs. 1.5. stationary distributions. #1 introduction to markov chain | complete course on mc | in this lecture series i will discuss complete markov chain , all the properties of markov chain , results , pyqs of csir.

Week 1 Lecture 1 Markov Chains Course Course description course description : this course is an introduction to markov chains, random walks, martingales. Example 1. a colleague travels between four coee shops located as follows: 3 4 ach path as equally likely. if we model our colleague’s journey as a markov chain, then a suitable state space would be s = {1, 2, 3, 4} and the transition 0 1 0 0 = p 1 3. In this section we give the definition of a markov chain and several related concepts. In order to represent the weather in our example as a markov chain, we need to perform a trick that is sometimes called markovian lift. the idea is to consider the weather on two consecutive days together.
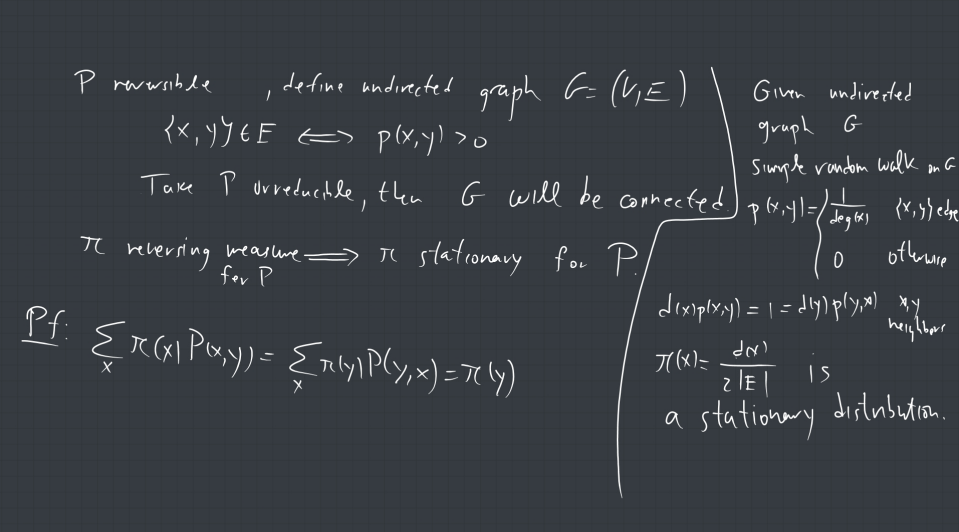
Week 1 Lecture 1 Markov Chains Course In this section we give the definition of a markov chain and several related concepts. In order to represent the weather in our example as a markov chain, we need to perform a trick that is sometimes called markovian lift. the idea is to consider the weather on two consecutive days together. De nition 1.1 a sequence of random variables (xn) is called a markov chain if the past and future of the process are conditionally independent given the present. The transition graph of the chain is the oriented graph where vertices are states and an arrow from i to j exists if and only if pij > 0, taking value pij when it exists. Example 14. (apply to markov chains) here we start with a markov chain fxkg1 k=0, and we make a copy of it denoted fykg1 k=0, with the joint distribution speci ed later. Explore the theoretical foundations of utilizing markov chains in computational applications before they reach their mixing time in this lecture from a specialized discussion meeting on geometry, probability, and algorithms.

Week 1 Lecture 1 Markov Chains Course De nition 1.1 a sequence of random variables (xn) is called a markov chain if the past and future of the process are conditionally independent given the present. The transition graph of the chain is the oriented graph where vertices are states and an arrow from i to j exists if and only if pij > 0, taking value pij when it exists. Example 14. (apply to markov chains) here we start with a markov chain fxkg1 k=0, and we make a copy of it denoted fykg1 k=0, with the joint distribution speci ed later. Explore the theoretical foundations of utilizing markov chains in computational applications before they reach their mixing time in this lecture from a specialized discussion meeting on geometry, probability, and algorithms.
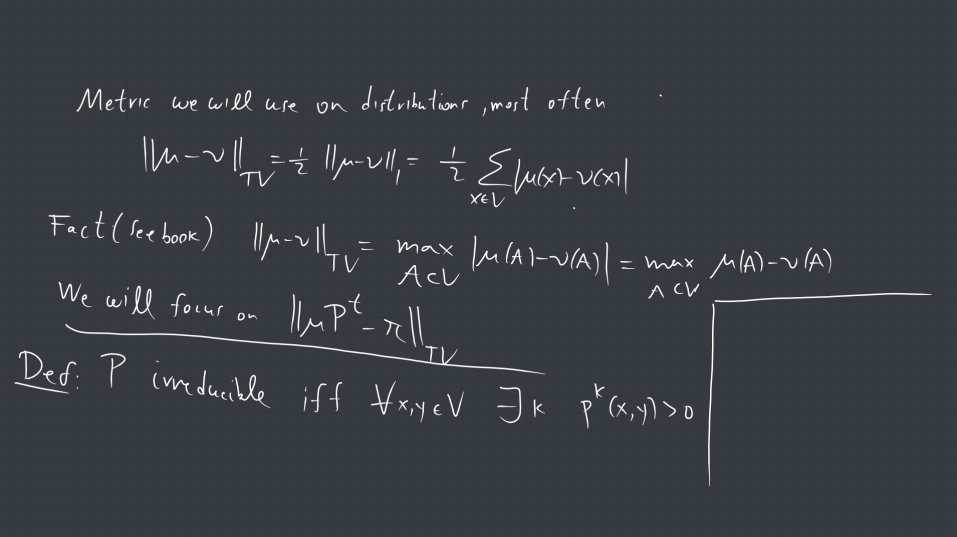
Week 1 Lecture 1 Markov Chains Course Example 14. (apply to markov chains) here we start with a markov chain fxkg1 k=0, and we make a copy of it denoted fykg1 k=0, with the joint distribution speci ed later. Explore the theoretical foundations of utilizing markov chains in computational applications before they reach their mixing time in this lecture from a specialized discussion meeting on geometry, probability, and algorithms.
Comments are closed.