Vector Spaces Coordinate Systems The Change Of Coordinates Matrix

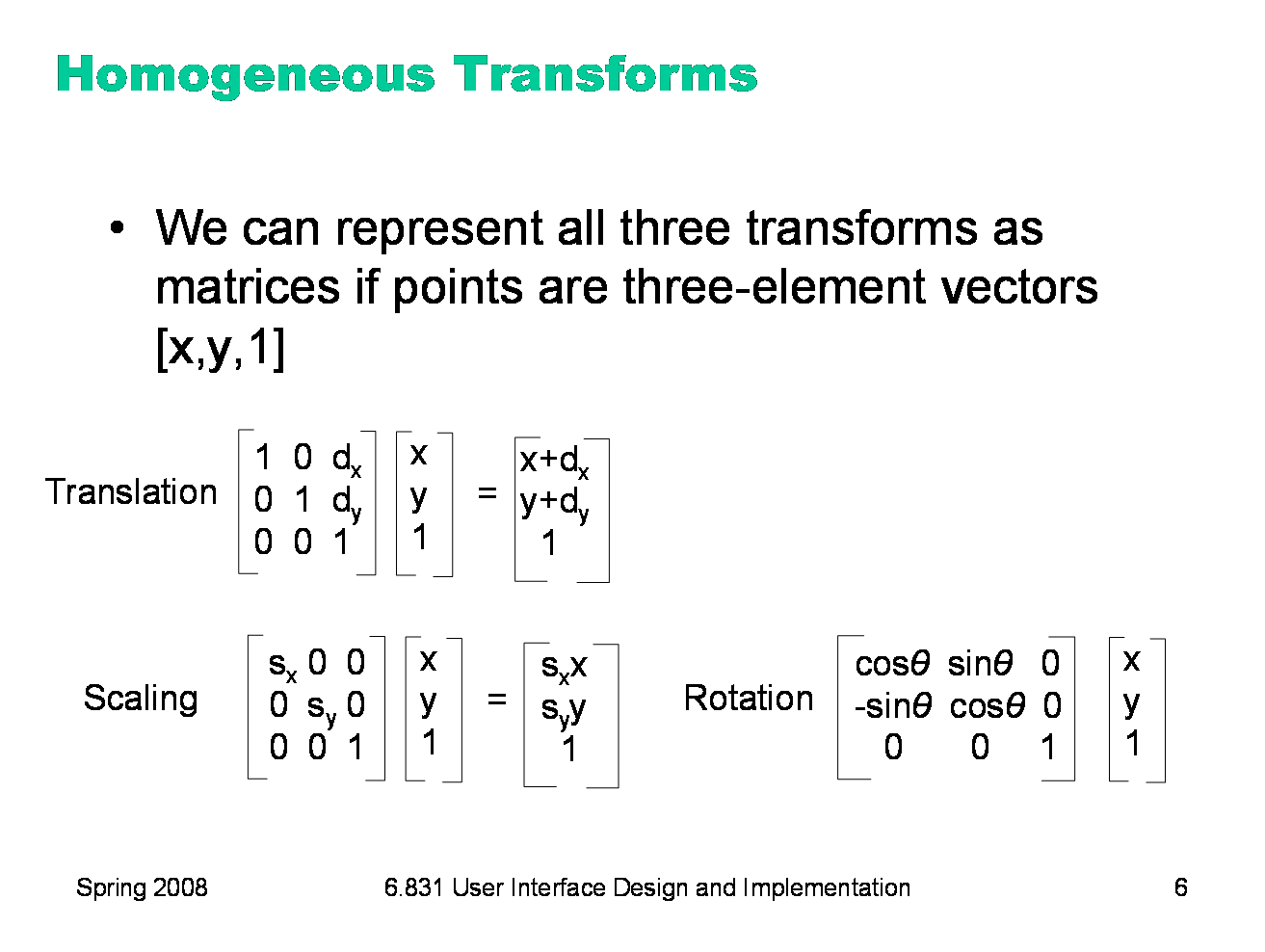
Basis Dimensions In Vector Spaces A Practical Approach In v = rn, the standard basis creates the standard coordinate system (the one we usually use for rn). some other vector spaces also have a standard basis, f r instance pd(t) or rm n, but most vector spaces don't, so we can't depend on hav. Matrices have two purposes (at least for geometry) transform things e.g. rotate the car from facing north to facing east express coordinate system changes e.g. given the driver's location in the coordinate system of the car, express it in the coordinate system of the world.
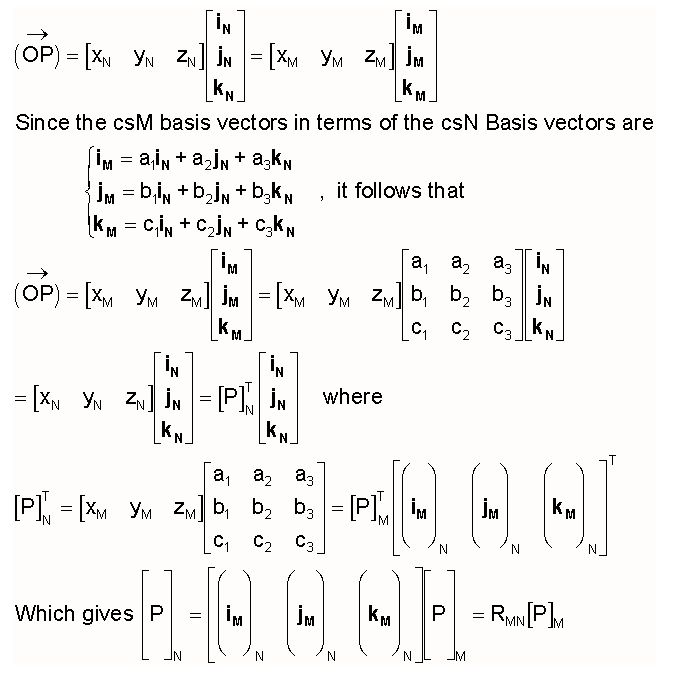
Coordinate Vector At Vectorified Collection Of Coordinate Vector Em, and a different set in another. think of a street corner in manhattan: the pair (street, avenue) is one set of coordinates, a d (latitude, longitude) is another. today we’ll talk about how to translate from one coordinate system to another, by. Change of coordinates matrix a change of coordinates matrix, also called a transition matrix, specifies the transformation from one vector basis to another under a change of basis. Given coordinates of a point in one basis, we will be able to obtain the coordinates of that point in another basis by applying the change of coordinates matrix to it. Change of bases isaiah lankham, bruno nachtergaele, anne schilling (march 8, 2007) re in one to basis for the vector space, however. in this lecture we address the question how the matrix for a linear operator changes if we change f.
Coordinate Vector At Vectorified Collection Of Coordinate Vector Given coordinates of a point in one basis, we will be able to obtain the coordinates of that point in another basis by applying the change of coordinates matrix to it. Change of bases isaiah lankham, bruno nachtergaele, anne schilling (march 8, 2007) re in one to basis for the vector space, however. in this lecture we address the question how the matrix for a linear operator changes if we change f. Example 5: in the vector space p3, consider the two bases = 1 2t 3t2 4t3, 2t 3t2, 1 2t, 1 and = c t3,. The coordinate mapping in theorem 8 is an important example of an isomorphism from v onto rn. in general, a 1 1 linear transformation from a vector space v onto a vector space w is called an isomorphism from v onto w. R3, which are the coordinate maps for bases ~b1; ~b2; ~b3 and ~c1;~c2;~c3 respectively, then the mapping st 1 is defined as a mapping from r3 to r3. this mapping is linear, one–to–one and onto. Let v be an n dimensional real (or complex) vector space. vectors that live in are usually represented by a single column of n real (or complex) numbers. a linear transformation (also called a linear operator) acting on v is a “machine” that acts on a vector and and produces another vector.

Coordinate Systems And Transformations And Vector Calculus Example 5: in the vector space p3, consider the two bases = 1 2t 3t2 4t3, 2t 3t2, 1 2t, 1 and = c t3,. The coordinate mapping in theorem 8 is an important example of an isomorphism from v onto rn. in general, a 1 1 linear transformation from a vector space v onto a vector space w is called an isomorphism from v onto w. R3, which are the coordinate maps for bases ~b1; ~b2; ~b3 and ~c1;~c2;~c3 respectively, then the mapping st 1 is defined as a mapping from r3 to r3. this mapping is linear, one–to–one and onto. Let v be an n dimensional real (or complex) vector space. vectors that live in are usually represented by a single column of n real (or complex) numbers. a linear transformation (also called a linear operator) acting on v is a “machine” that acts on a vector and and produces another vector.

Solved Consider The System Of Vectors Find The Change Of Chegg R3, which are the coordinate maps for bases ~b1; ~b2; ~b3 and ~c1;~c2;~c3 respectively, then the mapping st 1 is defined as a mapping from r3 to r3. this mapping is linear, one–to–one and onto. Let v be an n dimensional real (or complex) vector space. vectors that live in are usually represented by a single column of n real (or complex) numbers. a linear transformation (also called a linear operator) acting on v is a “machine” that acts on a vector and and produces another vector.
Comments are closed.