Using The Horizontal Line Test To Determine If A Function Is One To One

Solved Using The Horizontal Line Test Determine Whether The Chegg A graph passes the horizontal test if every horizontal line crosses, or intersects it, at one or fewer points. if the graph passes the test, it is a one to one function – every specific input corresponds to exactly one output. If a function passes the horizontal line test, then no horizontal line will cross the graph more than once, and the graph is said to be one to one. this graph doesn't pass the horizontal line test because any horizontal line between ???y= 2??? and ???y=2??? would intersect it more than once.

Solved Using The Horizontal Line Test Determine Whether The Chegg Step by step tutorial explains how to determine if a function is a one to one function using the horizontal line test. ace your math exam!. How to: given a graph of a function, use the horizontal line test to determine if the graph represents a one to one function. inspect the graph to see if any horizontal line drawn would intersect the curve more than once. This precalculus video tutorial explains how to determine if a graph has an inverse function using the horizontal line test. if it passes the test, the function is a one to one. Learn how to identify one to one functions using the horizontal line test. this comprehensive guide includes step by step instructions, examples, and practice problems to help you master this concept.
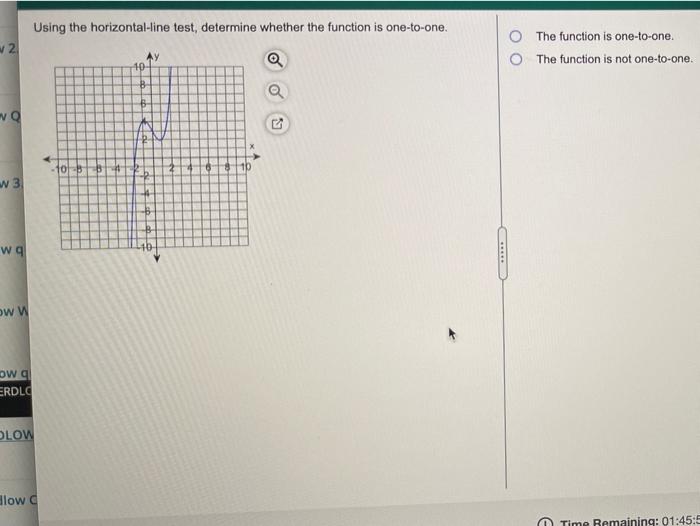
Solved Using The Horizontal Line Test Determine Whether The Chegg This precalculus video tutorial explains how to determine if a graph has an inverse function using the horizontal line test. if it passes the test, the function is a one to one. Learn how to identify one to one functions using the horizontal line test. this comprehensive guide includes step by step instructions, examples, and practice problems to help you master this concept. If the graph passes the horizontal line test, then the function is one to one. if the graph fails the horizontal line test, then the function is not one to one, even though it might pass the vertical line test. With this test, you can see if any horizontal line drawn through the graph cuts through the function more than one time. if the line passes through the function more than once, the function fails the test and therefore isn't a one to one function. Given a graph of a function, use the horizontal line test to determine if the graph represents a one to one function. inspect the graph to see if any horizontal line drawn would intersect the curve more than once. So, there is one new characteristic that must be true for a function to be one to one. this new requirement can also be seen graphically when we plot functions, something we will look at below with the horizontal line test.
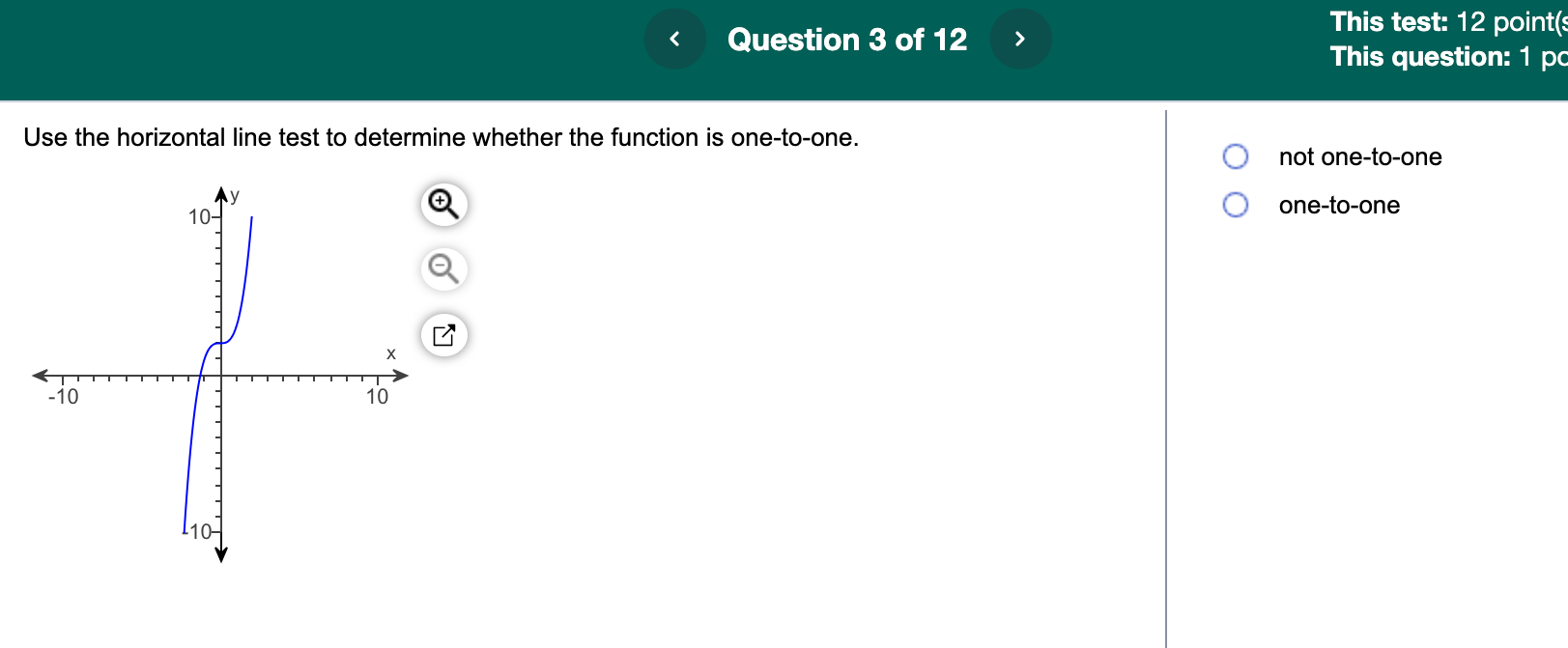
Solved Use The Horizontal Line Test To Determine Whether The Chegg If the graph passes the horizontal line test, then the function is one to one. if the graph fails the horizontal line test, then the function is not one to one, even though it might pass the vertical line test. With this test, you can see if any horizontal line drawn through the graph cuts through the function more than one time. if the line passes through the function more than once, the function fails the test and therefore isn't a one to one function. Given a graph of a function, use the horizontal line test to determine if the graph represents a one to one function. inspect the graph to see if any horizontal line drawn would intersect the curve more than once. So, there is one new characteristic that must be true for a function to be one to one. this new requirement can also be seen graphically when we plot functions, something we will look at below with the horizontal line test.
Comments are closed.