U5 6 Maxima And Minima Of Functions Of Two Variables Pdf Maxima And

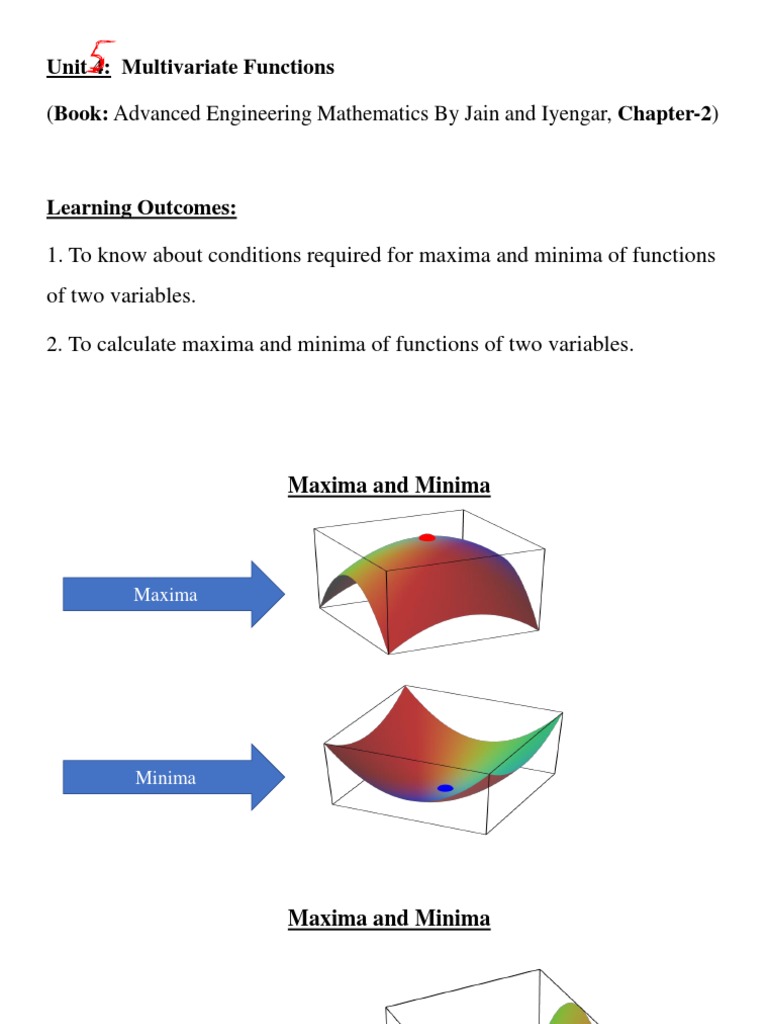
U5 6 Maxima And Minima Of Functions Of Two Variables Pdf Maxima And 1. the document discusses functions of two variables and how to determine if a critical point is a relative maximum, minimum, or saddle point. 2. it provides the conditions to check: the critical point must satisfy fx=0 and fy=0, then calculate fxx, fyy, fxy and check if rt s^2 is positive negative and the signs of r and t. 3. Similar to the extreme value theorem of single variable functions, a function of two variables f(x, y) attains both an absolute maximum and an absolute minimum on any closed, bounded set s where it is continuous.

Maxima And Minima Of Function Of One Variables Iit Jee Main It’s okay to divide out common factors which are numbers, but you should avoid dividing by something with a variable in it — unless you’re certain the expression cannot be zero. Example. find the absolute maximum and mini mum values of the function f (x, y) = 2 2x 2y − x2 − y2 on the triangular region in the first quadrant bounded 0, y = 0,. Extreme value theorem for functions of two variables if f is continuous on a closed, bounded set d in r2; then f attains an absolute maximum value f(x1; y1) and an absolute minimum value f(x2; y2) at some points (x1; y1) and (x2; y2) in d:. Maxima and minima of function of two variables r2 = {( , ) ∶ , } let , ( ) be a function of two variable defined on whole of r2.

Share Unit 2 Functions Of Several Variables Pdf Maxima And Minima Extreme value theorem for functions of two variables if f is continuous on a closed, bounded set d in r2; then f attains an absolute maximum value f(x1; y1) and an absolute minimum value f(x2; y2) at some points (x1; y1) and (x2; y2) in d:. Maxima and minima of function of two variables r2 = {( , ) ∶ , } let , ( ) be a function of two variable defined on whole of r2. Critical points are candidates for maxima and minima again because of fermat's principle: if rf(x0; y) 6= h0; 0i, then we can increase f by looking at the point (x0; y0) trf(x0; y0) for small t > 0 and get a larger value. Question find the critical points of the following functions and test for maxima and minima. We will begin by working out how to nd the local and absolute extrema (maxima and minima) of two variable functions by generalizing the concept of critical points to three dimensions. we will then turn to optimization problems. The document discusses the concepts of maxima and minima for functions of two variables, defining relative maximum and minimum points, as well as saddle points.