The Similarity Distance On Graphs And Graphons
Visual Comparison Of A The Similarity Distance Graphs Based On Human The similarity distance measures how “similar” two nodes in a dense graph are. selecting an epsilon net with respect to this metric is a useful tool in algorithms for very large graphs. The similarity distance measures how "similar" two nodes in a dense graph are. selecting an epsilon net with respect to this metric is a useful tool in algorithms for very large graphs.

The Similarity Distance On Graphs And Graphons Microsoft Research Testing by sampling lets say we have two graphs, g and h, and we want to say they are "similar" even though they're of radically di erent sizes. one idea is to compare whether the two have certain statistics that are close. The distance measures we define turn out be closely related to the cut distance. we establish our main results by generalizing our definitions to graphons, which are limit objects of sequences of graphs, as this allows us to apply techniques from functional analysis. The distance between g 1 and g 2 is defined by d (g 1, g 2) = min {d ϕ (g 1, g 2)}, where the minimum is taken over all one to one mappings ϕ from v (g 1) to v (g 2). it is shown that this distance is a metric on the space of connected graphs of a fixed order. In this work, we compare commonly used graph metrics and distance measures, and demonstrate their ability to discern between common topological features found in both random graph models and real world networks.
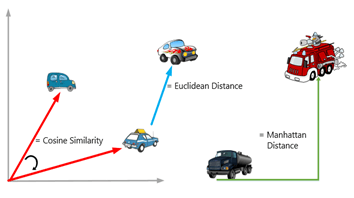
Similarity Distance Measures Intellify Solutions The distance between g 1 and g 2 is defined by d (g 1, g 2) = min {d ϕ (g 1, g 2)}, where the minimum is taken over all one to one mappings ϕ from v (g 1) to v (g 2). it is shown that this distance is a metric on the space of connected graphs of a fixed order. In this work, we compare commonly used graph metrics and distance measures, and demonstrate their ability to discern between common topological features found in both random graph models and real world networks. In this section, with the help of pattern distance, area based edge distance and position based edge distance, global distance will be proposed. afterwards, an algorithm is given to compute the distance between two graph data. It is customary to build this up from graphs, but it may be easier to grasp it starting from the way it works with graphons, and then go down to the graph case. Our precise notion of graph limit requires our use of a uniform probability measure on the vertex set. However, surprisingly little is known today about models to compare complex graphs, and quantitatively measure their similarity. this paper proposes a natural similarity measure for com plex networks: centrality distance, the di erence between two graphs with respect to a given node centrality.
Comments are closed.