The Difference Between Disk Washer And Shell Method

Know The Difference Between Disk Method Washer Method And Shell In calculus, the disk washer and shell methods are two separate integration processes used to find the volume of a solid of revolution. a solid of revolution is defined as a three dimensional shape created when an area, bounded by curves, axes, and or lines, is rotated around an axis of revolution. The shell and washer methods are no greater in complexity than the two different ways to compute the area of the region — you use the same bounding curves, and you use the same limits of integration.

Know The Difference Between Disk Method Washer Method And Shell When to use shell vs washer method: learn the difference between the shell method and washer method for calculating volume of solids of revolution, and when to use each method. The main difference between the disk, washer, and shell methods in calculus is that they all use different approaches to approximating a curve. the disk method uses a circular region around an approximation of the curve, while the washer uses a region shaped like a washer when viewed from above. I will show you the differences between the disk washer and the cylindrical shell method. most importantly, you need to know when to use which method in different situations. If you want to find the volume of the shape obtained when rotating the region bound by $f (x)$, $y=1$, and $x=2$ about the $y$ axis, then you would use the washer method since the shape you get after rotating has a "hole" in it.
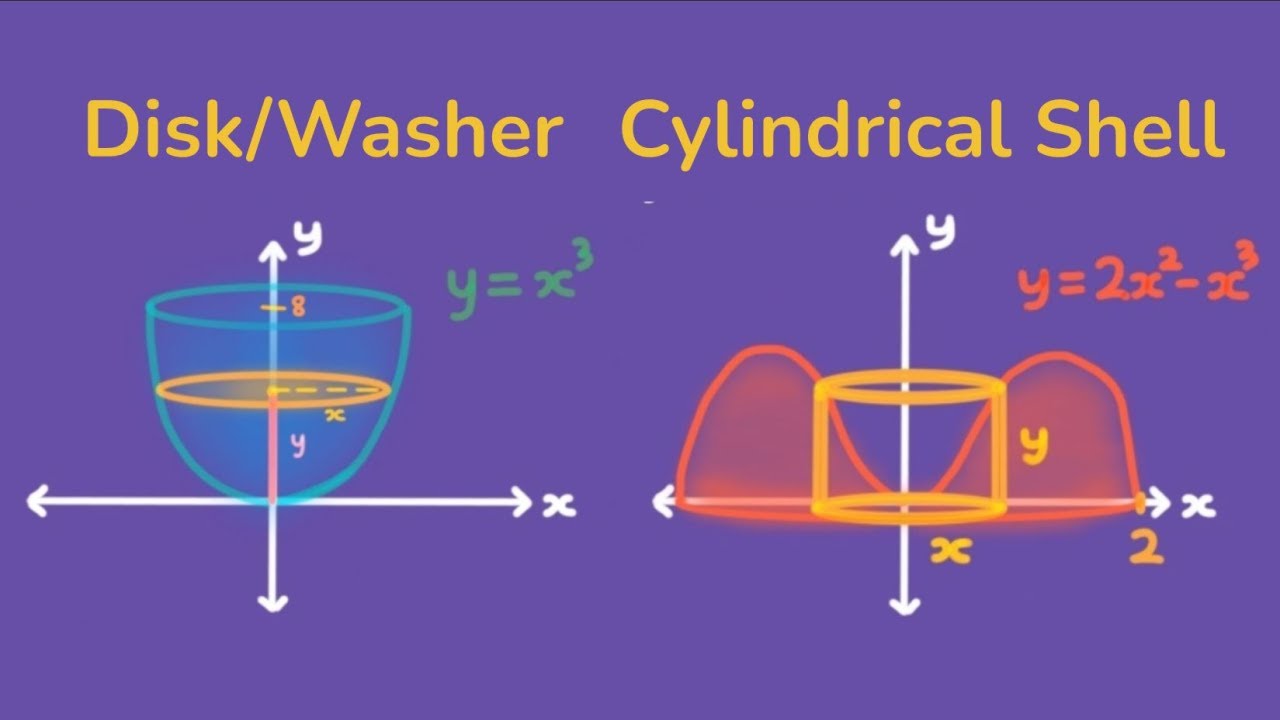
Difference Between Washer Method And Disk Method At Tyler Hale Blog I will show you the differences between the disk washer and the cylindrical shell method. most importantly, you need to know when to use which method in different situations. If you want to find the volume of the shape obtained when rotating the region bound by $f (x)$, $y=1$, and $x=2$ about the $y$ axis, then you would use the washer method since the shape you get after rotating has a "hole" in it. Use the disk method when there’s no hole and the shape touches the axis of rotation. use the washer method when there’s a hole or gap between the shape and the axis. The washer method is used when the rectangle sweeps out a solid that is similar to a cd (hole in the middle). and finally, the shell method is used when the rectangle sweeps out a solid that is similar to a toilet paper tube. The method of cylindrical shells and the disk washer methods are two techniques used in calculus to find the volumes of solids of revolution. though both aim to achieve the same goal, they do so using different approaches, and knowing when to use each can simplify the process. Example: volume between the functions y=x and y=x3 from x=0 to 1 these are the functions: rotated around the x axis: the disks are now "washers": and they have the area of an annulus: in our case r = x and r = x3 in effect this is the same as the disk method, except we subtract one disk from another. and so our integration looks like:.
Comments are closed.