Table 1 From Reinforcing Neural Network Stability With Attractor

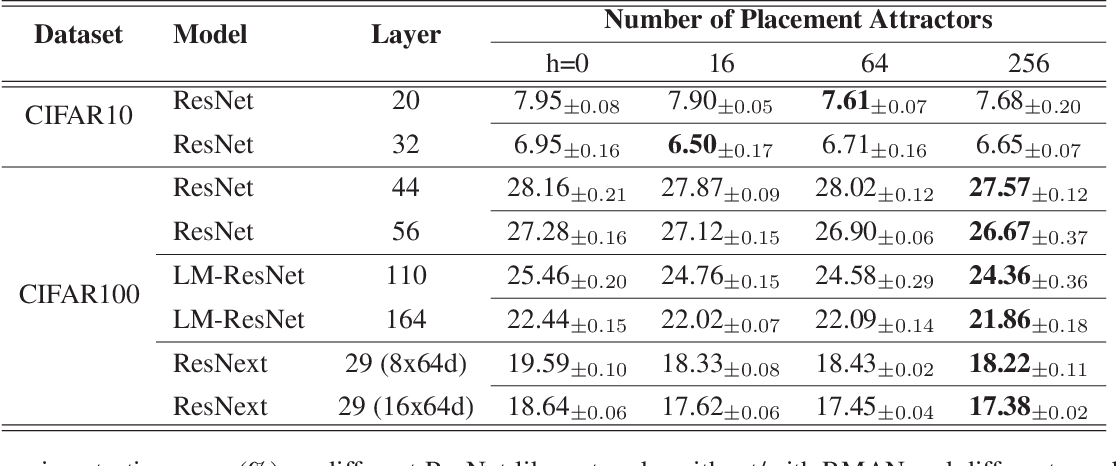
Table 1 From Reinforcing Neural Network Stability With Attractor This paper relates the exploding and vanishing gradient phenomenon to the stability of the discrete ode and presents several strategies for stabilizing deep learning for very deep networks. Through intensive experiments, we show that rman modified attractor dynamics bring a more structured representation space to resnet and its variants, and more importantly improve the generalization ability of resnet like networks in supervised tasks due to reinforced stability.

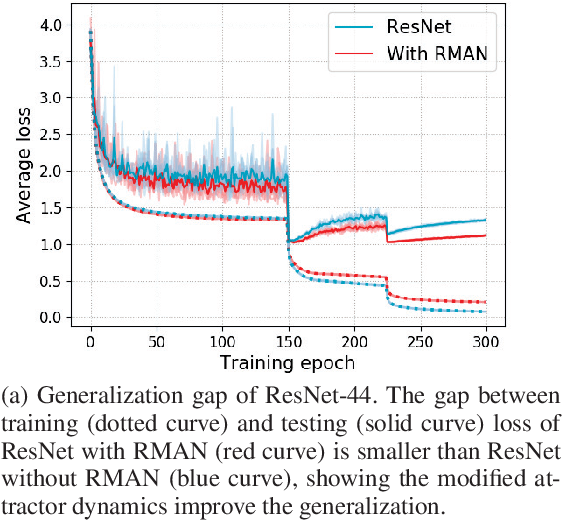
Figure 1 From Reinforcing Neural Network Stability With Attractor Table 1: comparison testing error (%) on different resnet like networks without with rman and different number of place ment attractors, where h = 0 denotes networks trained without rman. In this paper, we propose a novel relu max attractor network (rman) to model the attractor dynamics to reinforce sys tem stability of a deep neural network. rman is ready to be deployed on the state of the art resnets like network and it is only required during training stage. Attractor neural networks such as the hopfield model can be used to model associative memory. an efficient associative memory should be able to store a large number of patterns which must all be stable. we study in detail the meaning and definition of stability of network states. We propose to reinforce network stability of resnet and its variants by modeling their attractor dynamics so that the network can learn a better distribution of stable repre sentation.

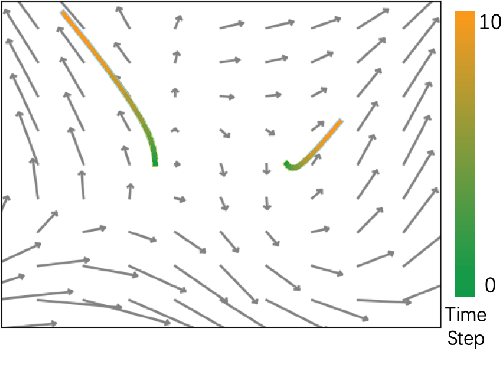
Figure 1 From Reinforcing Neural Network Stability With Attractor Attractor neural networks such as the hopfield model can be used to model associative memory. an efficient associative memory should be able to store a large number of patterns which must all be stable. we study in detail the meaning and definition of stability of network states. We propose to reinforce network stability of resnet and its variants by modeling their attractor dynamics so that the network can learn a better distribution of stable repre sentation. In these lecture notes, we review four key examples that demonstrate how autoassociative neural network models can elucidate the computational mechanisms underlying attractor based information processing in biological neural systems performing cognitive functions. To overcome this difficulty, a solution is to include adaptation in the attractor network dynamics, whereby the adaptation serves as a slow negative feedback mechanism to destabilize what are otherwise permanently stable states. In this paper, we take a step further to be the first to reinforce this stability of dnns without changing their original structure and verify the impact of the reinforced stability on. Here, we derive a theory of the local stability of discrete fixed points in a broad class of networks with graded neural activities and in the presence of noise.

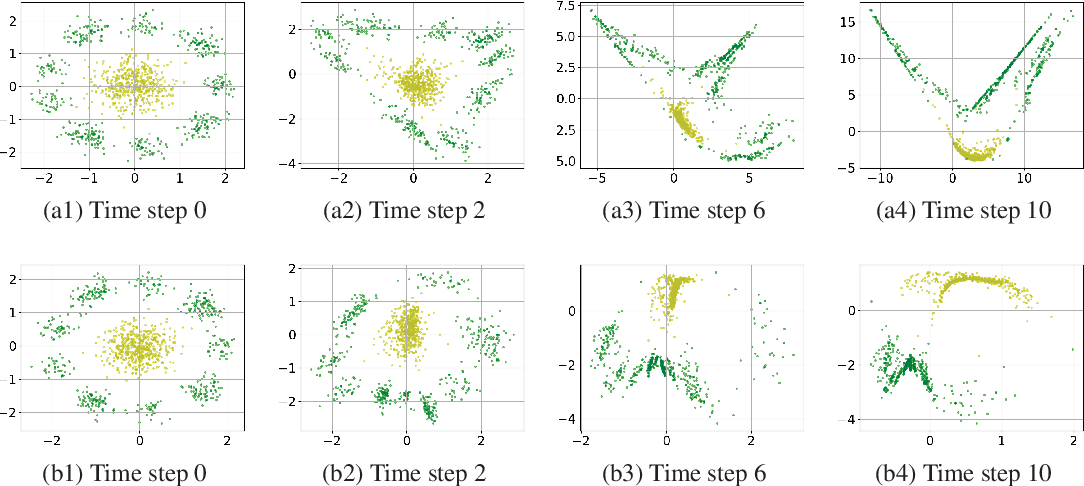
Figure 2 From Reinforcing Neural Network Stability With Attractor In these lecture notes, we review four key examples that demonstrate how autoassociative neural network models can elucidate the computational mechanisms underlying attractor based information processing in biological neural systems performing cognitive functions. To overcome this difficulty, a solution is to include adaptation in the attractor network dynamics, whereby the adaptation serves as a slow negative feedback mechanism to destabilize what are otherwise permanently stable states. In this paper, we take a step further to be the first to reinforce this stability of dnns without changing their original structure and verify the impact of the reinforced stability on. Here, we derive a theory of the local stability of discrete fixed points in a broad class of networks with graded neural activities and in the presence of noise.

Figure 2 From Stability Analysis Of Attractor Neural Network Model Of In this paper, we take a step further to be the first to reinforce this stability of dnns without changing their original structure and verify the impact of the reinforced stability on. Here, we derive a theory of the local stability of discrete fixed points in a broad class of networks with graded neural activities and in the presence of noise.