Solving Systems Of Equations Using Determinants With Two And Three

Solving Systems Of Linear Equations In Three Variables Using Here we will demonstrate the rule for both systems of two equations with two variables and for systems of three equations with three variables. let’s start with the systems of two equations with two variables. It can be derived by solving the general form of the systems of equations by elimination. here we will demonstrate the rule for both systems of two equations with two variables and for systems of three equations with three variables.

Solving Systems Of Linear Equations In Three Variables Using A system of linear equations having two and three variables can be easily solved using determinants. here, the formulas and steps to find the solution of a system of linear equations are given along with practice problems. To use determinants to solve a system of three equations with three variables (cramer's rule), say x, y, and z, four determinants must be formed following this procedure:. Problems involving linear system solution are found on other pages linked through the algebra page. the linear system solver page goes through a step by step solution using determinants. Determinants are useful in solving systems of equations in two (and later, three) variables. the use of determinants to solve a system of equations is known as cramer’s rule. let’s learn how to solve a system of 2x2 equations using cramer’s rule.
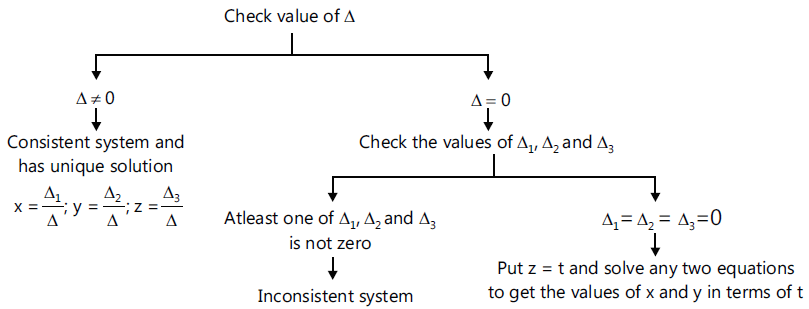
Solving Systems Of Linear Equations In Three Variables Using Problems involving linear system solution are found on other pages linked through the algebra page. the linear system solver page goes through a step by step solution using determinants. Determinants are useful in solving systems of equations in two (and later, three) variables. the use of determinants to solve a system of equations is known as cramer’s rule. let’s learn how to solve a system of 2x2 equations using cramer’s rule. We have learned how to solve systems of equations in two variables and three variables, and by multiple methods: substitution, addition, gaussian elimination, using the inverse of a matrix, and graphing. Now that we can find the determinant of a 3 × 3 matrix, we can apply cramer’s rule to solve a system of three equations in three variables. cramer’s rule is straightforward, following a pattern consistent with cramer’s rule for 2 × 2 matrices. Here we will demonstrate the rule for both systems of two equations with two variables and for systems of three equations with three variables. let’s start with the systems of two equations with two variables. In this video, we bring together everything we've learnt in the chapters of matrices and determinants. we find the solution of a system of equations using the matrix method. we first.

Solving Systems Of Linear Equations In Three Variables Using We have learned how to solve systems of equations in two variables and three variables, and by multiple methods: substitution, addition, gaussian elimination, using the inverse of a matrix, and graphing. Now that we can find the determinant of a 3 × 3 matrix, we can apply cramer’s rule to solve a system of three equations in three variables. cramer’s rule is straightforward, following a pattern consistent with cramer’s rule for 2 × 2 matrices. Here we will demonstrate the rule for both systems of two equations with two variables and for systems of three equations with three variables. let’s start with the systems of two equations with two variables. In this video, we bring together everything we've learnt in the chapters of matrices and determinants. we find the solution of a system of equations using the matrix method. we first.

Solving Systems Of Linear Equations In Three Variables Using Here we will demonstrate the rule for both systems of two equations with two variables and for systems of three equations with three variables. let’s start with the systems of two equations with two variables. In this video, we bring together everything we've learnt in the chapters of matrices and determinants. we find the solution of a system of equations using the matrix method. we first.
Comments are closed.