Solving Practical Problems For Continuous Uniform Distribution Using Pdf Lecture 19

Continuous Uniform Distribution Pdf Solving practical problems for continuous uniform distribution using pdf || lecture # 19welcome to our video on solving practical problems for the co. Applications of the exponential distribution occurs naturally when describing the waiting time in a homogeneous poisson process. it can be used in a range of disciplines including queuing theory, physics, reliability theory, and hydrology.

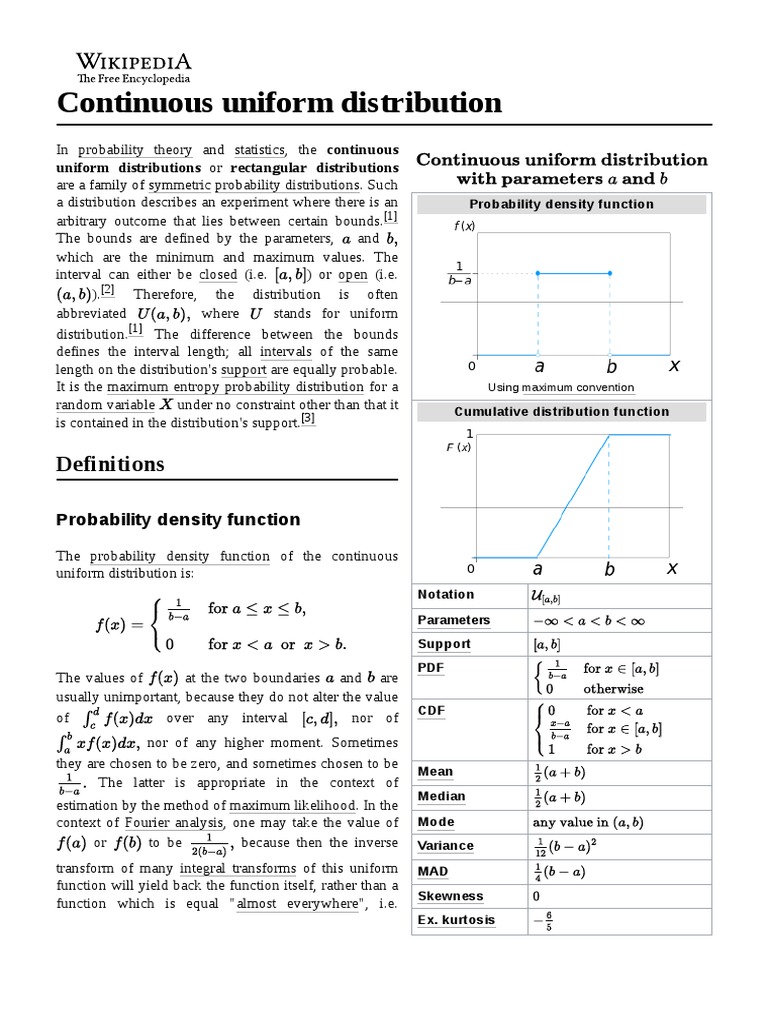
06 The Continuous Uniform Distribution Pdf Probability Distribution For a continuous uniform distribution on an interval, the “probability mass” is spread out evenly on that interval. pieces of the interval that have equal width will correspond to equal probabilities. Example 6.10. the length of human pregnancies from conception to birth varies according to a distribution that is approximately normal with mean 266 days and stan dard deviation 15 days. In a continuous setting (e.g. with time as a random variable), the probability the random variable of interest, say task length, takes exactly 5 minutes is infinitesimally small, hence p(x=5) = 0. This document describes the continuous uniform distribution and provides examples to illustrate key concepts. it defines the probability density function of a continuous uniform distribution over the interval [a,b] as f (x)=1 (b a) for a≤x≤b and 0 otherwise.

Understanding Continuous Uniform Distribution And Normal Course Hero In a continuous setting (e.g. with time as a random variable), the probability the random variable of interest, say task length, takes exactly 5 minutes is infinitesimally small, hence p(x=5) = 0. This document describes the continuous uniform distribution and provides examples to illustrate key concepts. it defines the probability density function of a continuous uniform distribution over the interval [a,b] as f (x)=1 (b a) for a≤x≤b and 0 otherwise. X is a continuous random variable with a uniform distribution between 0 and 3. It covers various distributions including binomial, geometric, poisson, and exponential, providing examples and problems for practical application. the inverse transformation method is highlighted as a key technique for simulating continuous random variables using uniform random numbers. 0 to and the sample is = length, a uniform distribution betwen including 23 seconds is ibutio in seconds, of an. In lessons 1 and 2 we will discuss the continuous uniform distribution and normal distribution. for these we will develop easier ways of solving for probabilities of interest.

Understanding Uniform Distribution Examples Probabilities Course Hero X is a continuous random variable with a uniform distribution between 0 and 3. It covers various distributions including binomial, geometric, poisson, and exponential, providing examples and problems for practical application. the inverse transformation method is highlighted as a key technique for simulating continuous random variables using uniform random numbers. 0 to and the sample is = length, a uniform distribution betwen including 23 seconds is ibutio in seconds, of an. In lessons 1 and 2 we will discuss the continuous uniform distribution and normal distribution. for these we will develop easier ways of solving for probabilities of interest.