Solving Constrained Optimization Problems Techniques Examples

Constrained Optimization Pdf Operations Research Teaching Mathematics In this section we will use a general method, called the lagrange multiplier method, for solving constrained optimization problems:. Learn constrained optimization methods, including direct substitution, constrained variation, lagrange multipliers, and kkt conditions, with examples for engineering and economics.

Constrained Optimization 1 Pdf Mathematical Optimization In this tutorial, we’ll provide a brief introduction to constrained optimization, explore some examples, and introduce some methods to solve constrained optimization problems. Maximize (or minimize) the function f (x, y) subject to the condition g(x, y) = 0. in some cases one can solve for y as a function of x and then find the extrema of a one variable function. Theorem for any starting point x0 the generated sequence fxkg is bounded and any of its cluster points is a global optimum. example. solve the problem 8 min < (x1 0 x1 3)2 (x2 1)2. Constrained optimization problems can be defined using an objective function and a set of constraints. n a feasible point is any point that fulfills all the constraints. n an optimal point is one that locally optimizes the value function given the constraints.
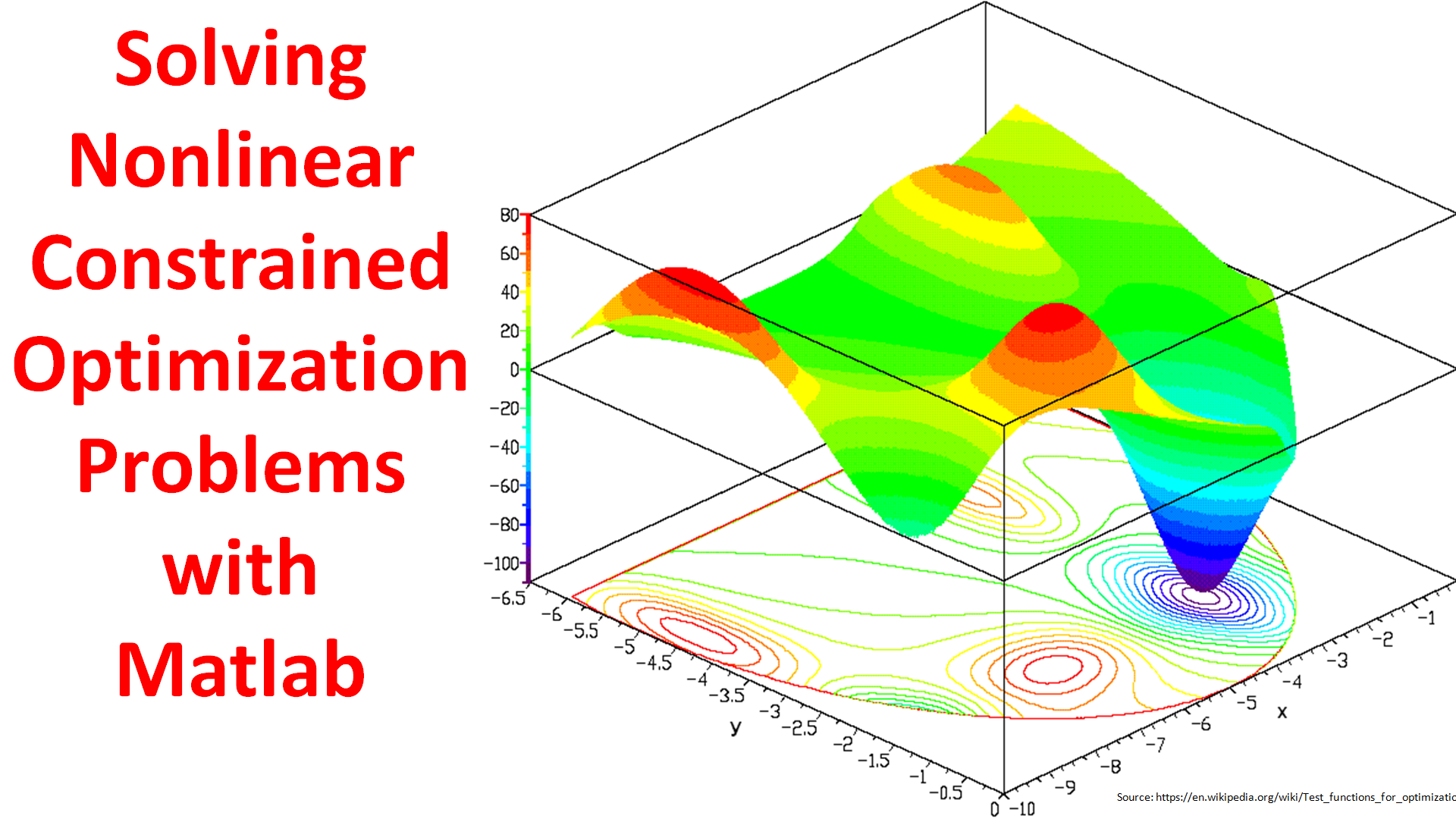
How To Solve Constrained Optimization Problems In Matlab Theorem for any starting point x0 the generated sequence fxkg is bounded and any of its cluster points is a global optimum. example. solve the problem 8 min < (x1 0 x1 3)2 (x2 1)2. Constrained optimization problems can be defined using an objective function and a set of constraints. n a feasible point is any point that fulfills all the constraints. n an optimal point is one that locally optimizes the value function given the constraints. The lagrange multipliers method and kkt conditions are powerful techniques for solving constrained optimization problems. advanced topics in constrained optimization include sensitivity analysis, constrained optimization with multiple constraints, and numerical methods for constrained optimization. Lagrange devised a strategy to turn constrained problems into the search for critical points by adding vari ables, known as lagrange multipliers. this section describes that method and uses it to solve some problems and derive some important inequalities. Imize f (x) subject to h(x) = 0 = fx 2 rn : h(x) = 0g. some equality constrained optimi. ation pr. 2x2 = 3 4x1 5x3 = 6 . he constraints imply that x2 = 2(3 x1) and x3 = 5(6 x1). substi tute x2 and x3 in the objective f. nction t. is equivalent to maximizing x2 1x2 2 . solving this is using 1 = x2 1 (2x2)2 4x1x2 where p p t. We will close our initial discussion of constrained convex optimization with a very brief tour of common categories of constrained convex optimization problems, giving a few practical examples where each arises.

How To Solve Constrained Optimization Problems In Matlab The lagrange multipliers method and kkt conditions are powerful techniques for solving constrained optimization problems. advanced topics in constrained optimization include sensitivity analysis, constrained optimization with multiple constraints, and numerical methods for constrained optimization. Lagrange devised a strategy to turn constrained problems into the search for critical points by adding vari ables, known as lagrange multipliers. this section describes that method and uses it to solve some problems and derive some important inequalities. Imize f (x) subject to h(x) = 0 = fx 2 rn : h(x) = 0g. some equality constrained optimi. ation pr. 2x2 = 3 4x1 5x3 = 6 . he constraints imply that x2 = 2(3 x1) and x3 = 5(6 x1). substi tute x2 and x3 in the objective f. nction t. is equivalent to maximizing x2 1x2 2 . solving this is using 1 = x2 1 (2x2)2 4x1x2 where p p t. We will close our initial discussion of constrained convex optimization with a very brief tour of common categories of constrained convex optimization problems, giving a few practical examples where each arises.

Constrained Optimization Numerical Examples Download Scientific Diagram Imize f (x) subject to h(x) = 0 = fx 2 rn : h(x) = 0g. some equality constrained optimi. ation pr. 2x2 = 3 4x1 5x3 = 6 . he constraints imply that x2 = 2(3 x1) and x3 = 5(6 x1). substi tute x2 and x3 in the objective f. nction t. is equivalent to maximizing x2 1x2 2 . solving this is using 1 = x2 1 (2x2)2 4x1x2 where p p t. We will close our initial discussion of constrained convex optimization with a very brief tour of common categories of constrained convex optimization problems, giving a few practical examples where each arises.
What Is Constrained Optimization Baeldung On Computer Science
Comments are closed.