Solved We Consider Events A B And C Which Can Occur In Chegg

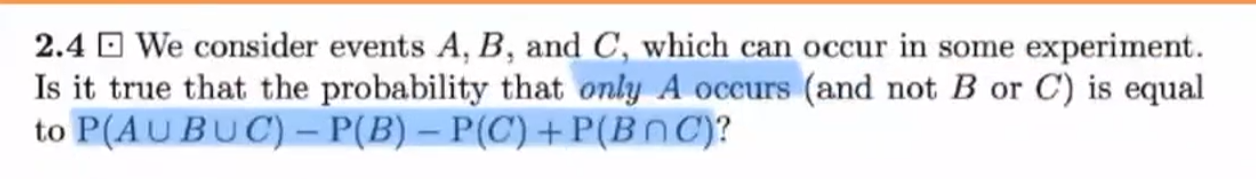
Solved 2 4 We Consider Events A B And C Which Can Occur Chegg Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. see answer. To determine if the statement is true, we need to analyze what is meant by the probability that only event a occurs (and not events b or c). this can be expressed mathematically as p (a ∩ b ∩ c), where b and c represent the complements of events b and c, respectively.

Solved We Consider Events A B And C Which Can Occur In Chegg Consider a sample space $s$ and three events $a$, $b$, and $c$. for each of the following events draw a venn diagram representation as well as a set expression. We are interested in the probability that only a occurs, which can be expressed as p (a ∖ (b ∪ c)). this represents the probability of a occurring while neither b nor c occurs. Suppose two events a and b are mutually exclusive, with p (a) ≠ 0 and p (b) ≠ 0. by working through the following steps, you'll see why two mutually exclusive events are not independent. Express c in terms of a and b, using only the basic operations "union," "intersection," and "complement." also draw a diagram to illustrate why your expression works.

Solved The Events A B And C Occur With Respective Chegg Suppose two events a and b are mutually exclusive, with p (a) ≠ 0 and p (b) ≠ 0. by working through the following steps, you'll see why two mutually exclusive events are not independent. Express c in terms of a and b, using only the basic operations "union," "intersection," and "complement." also draw a diagram to illustrate why your expression works. In the situation you described, where event a causes event b, and event b causes event c, event a would be the cause of event c if all three of the above conditions are satisfied. Our expert help has broken down your problem into an easy to learn solution you can count on. (1) for two or more events (a, b, or c) to occur, the expression will be a ∪ b ∪ c (a ∩ b ∩ c). in a venn diagram, this would be represented by the space covered by any two of the circles, as well as the intersection of all three, but subtracting the common area to avoid double counting. One important lesson here is that, generally speaking, conditional independence neither implies (nor is it implied by) independence. thus, we can have two events that are conditionally independent but they are not unconditionally independent (such as $a$ and $b$ above).