Solved Velocity And Tangent Lines Problem 5 1 Point Let Chegg

Solved Velocity And Tangent Lines Problem 5 1 Point Let Chegg Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. see answer. Identify the given equation of the curve and the point where you want to find the tangent line. substitute the x coordinate of the given point into the equation to find the corresponding y coordinate.

2 1 The Tangent Line And Velocity Problem Download Free Pdf Driving question to start: if we know the exact position of on object, how can we find its velocity?. In both cases (tangent line and instantaneous velocity) we are taking a limit as the denominator goes to zero, and the numerator is also zero when this happens. Goals: de ne, compute, and draw secant and tangent lines. interpret the slope of secant and tangent lines. Section 2.1 the tangent and velocity problems a to a curve is a line that touches the curve. it also has the same direction as the curve at the point where the curve and line touch.

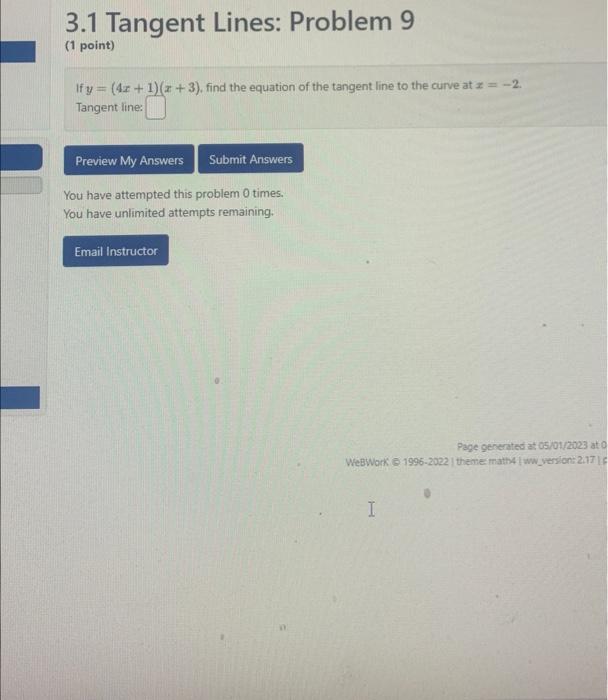
Solved 3 1 Tangent Lines Problem 3 5 Points Given Chegg Goals: de ne, compute, and draw secant and tangent lines. interpret the slope of secant and tangent lines. Section 2.1 the tangent and velocity problems a to a curve is a line that touches the curve. it also has the same direction as the curve at the point where the curve and line touch. Two such problems are: making sense of the slope at a point on a curve. finding the velocity of a moving object from knowing its position as a function of time. The equation of the tangent line at p is y = (1 point) consider the curve y = x2 2x 5. (a) find the slope of the secant line to the curve through the points p = (4, 29) and q = (4 h, (4 h)' 264 h) 5). Marius ionescu 2.1 the tangent and velocity problems. the angentt problem. the word tangent is derived from the latin word tangens, which means `touching.' thus, a tangent to a curve is a line that touches the curve. marius ionescu 2.1 the tangent and velocity problems. The theory of differential calculus historically stems from two different problems trying to determine the slope of a tangent line from its equation and trying to find the velocity of a moving object given its position as a function of time.