Solved Use This Theorem To Find The Inverse Of The Given Chegg

Solved Use This Theorem To Find The Inverse Of The Given Chegg Here’s the best way to solve it. find the inverse matrix … use this theorem to find the inverse of the given matrix or show that no inverse exists. Free inverse function calculator step by step solutions to help find the inverse of the function.

Solved Use This Theorem To Find The Inverse Of The Given Chegg An inverse function calculator makes finding inverses quick and easy, whether you’re a student, researcher, or professional. by understanding inverse functions and how to use these calculators, you can save time, avoid errors, and gain deeper insights into mathematical problems. First, we need to find the inverse laplace transform of the given function. the function is: $$ f (s) = \frac {s} {s^2 9} $$ we can use the theorem 7.2.1, which states that: $$ \mathcal {l}^ { 1}\ {f (s)\} = f (t) $$ to find the inverse laplace transform, we can use the table of laplace transforms and their inverses. The inverse transforms of the following could be computed using partial fractions. instead, find the inverse transform of each using the appropriate integration identity from section 25.3. How can we recover y(x)? the general problem of finding a function with a given laplace transform is called the inversion problem. this inversion problem and its applications to solving inital value problems is the topic of this lecture.

Solved Use Theorem 8 6 4 To Find The Inverse Of The Given Chegg The inverse transforms of the following could be computed using partial fractions. instead, find the inverse transform of each using the appropriate integration identity from section 25.3. How can we recover y(x)? the general problem of finding a function with a given laplace transform is called the inversion problem. this inversion problem and its applications to solving inital value problems is the topic of this lecture. Step 1 to find the inverse matrix, augment it with the identity matrix and perform row operations trying to. Since n1 and n2 are relatively prime, we know from bezout's lemma that we will be able to solve this equation for k and j. once we know k and j, we can then backsolve to give us a solution for x. Oh, i thought you were asking how to avoid the convolution theorem. it is not needed for the partial fraction decomposition. Given two integers a and m, find the modular multiplicative inverse of a under modulo m. the modular multiplicative inverse is an integer x such that: a x ≡ 1 (mod m).
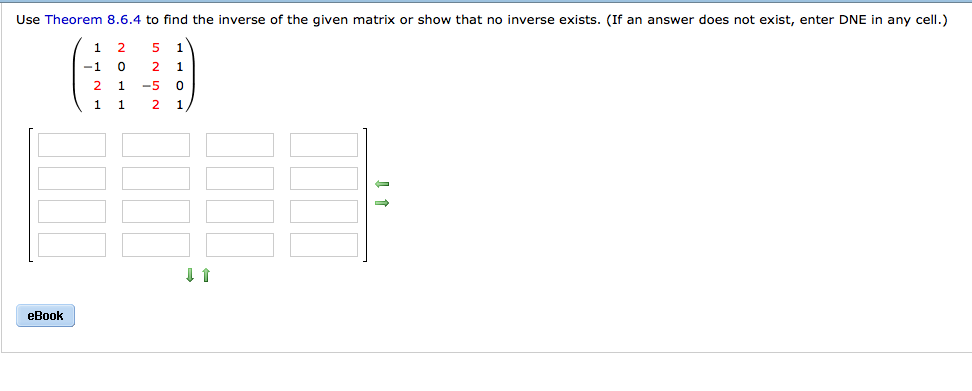
Solved Use Theorem 8 6 4 To Find The Inverse Of The Given Chegg Step 1 to find the inverse matrix, augment it with the identity matrix and perform row operations trying to. Since n1 and n2 are relatively prime, we know from bezout's lemma that we will be able to solve this equation for k and j. once we know k and j, we can then backsolve to give us a solution for x. Oh, i thought you were asking how to avoid the convolution theorem. it is not needed for the partial fraction decomposition. Given two integers a and m, find the modular multiplicative inverse of a under modulo m. the modular multiplicative inverse is an integer x such that: a x ≡ 1 (mod m).

Use Theorem 8 6 4 To Find The Inverse Of The Given Chegg Oh, i thought you were asking how to avoid the convolution theorem. it is not needed for the partial fraction decomposition. Given two integers a and m, find the modular multiplicative inverse of a under modulo m. the modular multiplicative inverse is an integer x such that: a x ≡ 1 (mod m).
Comments are closed.