Solved Use The Binomial Series To Expand The Function Chegg

Solved Use The Binomial Series To Expand The Function As A Chegg There are 3 steps to solve this one. consider the function f (x) = 1 x 5 . the binomial series expansion of (1 x) k is (1 x) k = ∑ n = 0 ∞ (k c n) x n implies (1 x) k = 1 k x k (k 1) 2! x 2 k (k 1) (k 2) 3! x 3 . substitute the values k = 1 5 and x = x. Learn how to use the binomial series to expand a function as a power series for four or five terms using easy to follow steps.

Solved Use The Binomial Series To Expand The Function As A Chegg In the context of binomial series, the power series expansion enables us to approximate a function by summing up its terms, making calculations and predictions more manageable. To solve this task, we have to use the binomial series to find a series expansion for the given function. what is the binomial series and how can we apply it?. The radius of convergence for the binomial series is given by the interval $|z| < 1$. in our case, $z = \frac {x} {8}$, so the radius of convergence is: $|\frac {x} {8}| < 1 \rightarrow |x| < 8$ thus, the radius of convergence is 8. Use the binomial series to expand the function as a maclaurin series and to find the first three taylor polynomials t1, t2, and t3. graph the function and these taylor polynomials in the interval of.

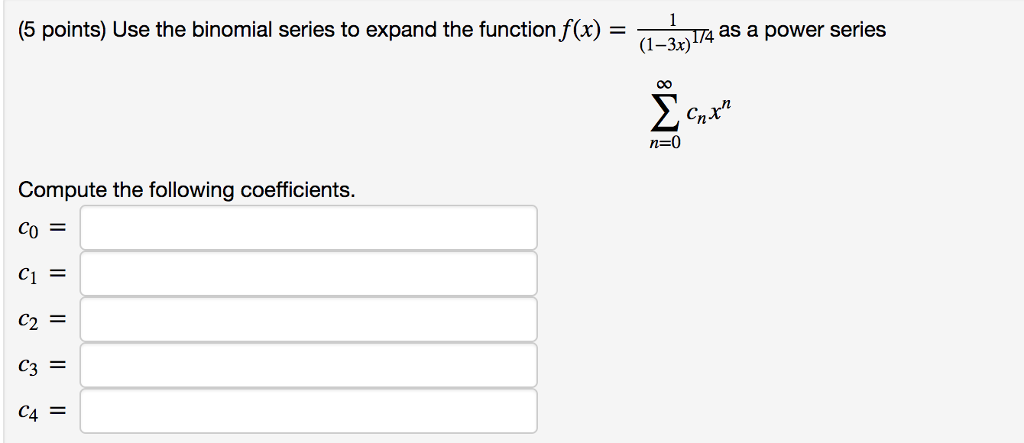
Solved 5 Points Use The Binomial Series To Expand The Chegg The radius of convergence for the binomial series is given by the interval $|z| < 1$. in our case, $z = \frac {x} {8}$, so the radius of convergence is: $|\frac {x} {8}| < 1 \rightarrow |x| < 8$ thus, the radius of convergence is 8. Use the binomial series to expand the function as a maclaurin series and to find the first three taylor polynomials t1, t2, and t3. graph the function and these taylor polynomials in the interval of. This section explores the binomial theorem in the context of taylor series and applies taylor series to expand binomial expressions with non integer exponents. it covers the use of taylor series in …. I'll solve this problem step by step using the binomial series expansion. expanding $\frac {5} {1 x}$ not the question you’re looking for? post any question and get expert help quickly. In the given exercise, the function is expanded into a power series using the binomial series, which helps in handling non integer exponents. the power series takes the form: this expansion helps simplify the function into terms that are polynomial, allowing easier manipulation and understanding. Use the binomial series to expand the function as a power series. state the radius of convergence. 1 (2 x) 3.

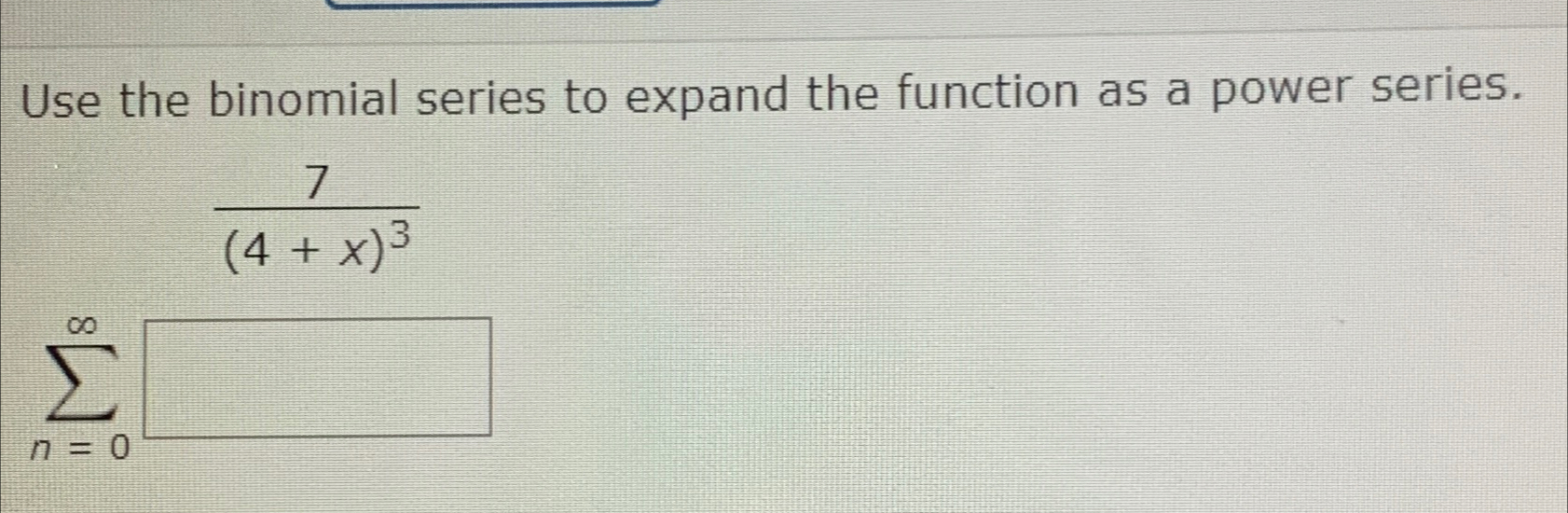
Solved Use The Binomial Series To Expand The Function As A Chegg This section explores the binomial theorem in the context of taylor series and applies taylor series to expand binomial expressions with non integer exponents. it covers the use of taylor series in …. I'll solve this problem step by step using the binomial series expansion. expanding $\frac {5} {1 x}$ not the question you’re looking for? post any question and get expert help quickly. In the given exercise, the function is expanded into a power series using the binomial series, which helps in handling non integer exponents. the power series takes the form: this expansion helps simplify the function into terms that are polynomial, allowing easier manipulation and understanding. Use the binomial series to expand the function as a power series. state the radius of convergence. 1 (2 x) 3.

Solved Use The Binomial Series To Expand The Function As A Chegg In the given exercise, the function is expanded into a power series using the binomial series, which helps in handling non integer exponents. the power series takes the form: this expansion helps simplify the function into terms that are polynomial, allowing easier manipulation and understanding. Use the binomial series to expand the function as a power series. state the radius of convergence. 1 (2 x) 3.