Solved Use Fourier Transform Method Chegg

Solved Use Fourier Transform Method Chegg Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. see answer question: use fourier transform method use fourier transform method. To recover u(x, t) we just need to take the inverse fourier transform. this is called the d’alembert form of the solution of the wave equation. the f(x − ct) part of the solution represents a wave packet moving to the right with speed c.
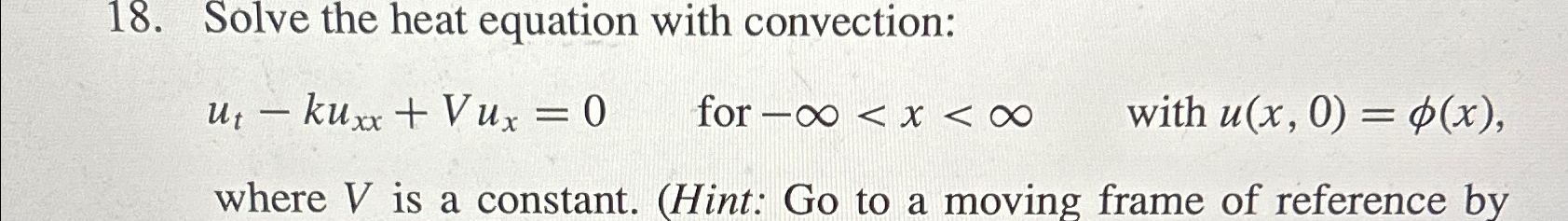
Solved Use Fourier Transform Method Chegg This note by a septuagenarian is an attempt to walk a nostalgic path and analytically solve fourier transform problems. half of the problems in this book are fully solved and presented in this note. To determine the coefficients c(ω) from (15) we need to introduce a couple of new concepts: fourier trans form and fourier integral representation of a function. Dirichlet’s conditions for existence of fourier transform fourier transform can be applied to any function if it satisfies the following conditions:. Solving the fourier transform equation for the dispersion of light from an object allows you to understand how light waves are spread out or scattered by the object.

Solved Use The Fourier Transform Analysis Equation To Chegg Dirichlet’s conditions for existence of fourier transform fourier transform can be applied to any function if it satisfies the following conditions:. Solving the fourier transform equation for the dispersion of light from an object allows you to understand how light waves are spread out or scattered by the object. Example solve the 1 d heat equation on an infinite rod, ut = c2uxx, −∞ < x < ∞, t > 0, u(x, 0) = f (x). we take the fourier transform (in x) on both sides to get ˆut = c2(iω)2 ˆu = −c2ω2 ˆu ˆu(ω, 0) = ˆf (ω). since there is only a t derivative, we solve as though ω were a constant: t) = a(ω)e−c2ω2t. The system d.c. gain is given by h(0) where h(s) is the system transfer function, which is equal the laplace transformation of h(t), i.e. the laplace transform of the system response to a unit impulse. At ^s solves a simple first order ode, ^st = dk2 ^s. the initial condition for this ode is given by the transform of (x x0), which by the translation property is e ix0k. Problem: how to use this to solve for u? main idea: if we could somehow write the above as a single fourier transform, that is ˆf (κ)e−dκ2t = ˆg(κ, t) for some g = g(x, t), then we’d get ˆu(κ, t) = ˆf (κ)e−dκ2t = ˆg(κ, t) and therefore u(x, t) = g(x, t).
Comments are closed.