Solved Theorem 8 4 2 Second Shifting Theorem If Aoen0 And Chegg

By healtycares On Aug 24, 2025

Solved The Second Shifting Theorem Replacing G By G 1 T Chegg Theorem 8.4.2 states that multiplying a laplace transform by the exponential e−τ s corresponds to shifting the argument of the inverse transform by τ units. To be able to work better with shifting, define a function, the unit step function, by u(t) = 0 for t < 0 and u(t) = 1 for t > 0. we now have l(u) = l(1) = 1. this is because the laplace transform only depends of on the values for t > 0.

Solved The Second Shifting Theorem Replacing G By G 1 T Chegg Here we’ll develop procedures to find laplace transforms of piecewise continuous functions, and to find the piecewise continuous inverses of laplace transforms, which will allow us to solve these initial value problems for \ (a>0\), the unit step function is given by. The second shifting property of laplace transforms is used to find the laplace of a function multiplied by a unit step function. let us discuss the second shifting property, its proof and some solved examples. I was of the understanding that the two shifts must be the same to solve this using the second shifting theorem. is it a typo in the question or how does one go about solving this?. Math calculus calculus questions and answers use the second shifting theorem to find the laplace transform of the following function.

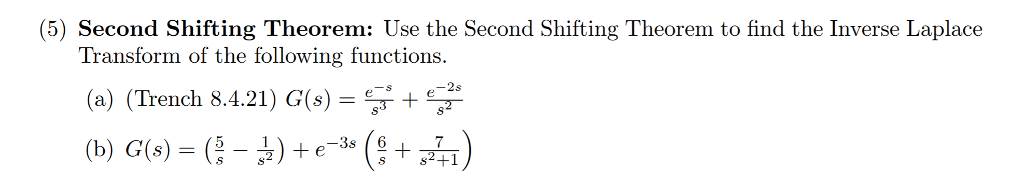
Solved 5 Second Shifting Theorem Use The Second Shifting Chegg I was of the understanding that the two shifts must be the same to solve this using the second shifting theorem. is it a typo in the question or how does one go about solving this?. Math calculus calculus questions and answers use the second shifting theorem to find the laplace transform of the following function. Second shifting property if $\mathcal {l} \left\ { f (t) \right\} = f (s)$, and $g (t) = \begin {cases} f (t a) & t \gt a \\ 0 & t \lt a \end {cases}$ then, $\mathcal {l} \left\ { g (t) \right\} = e^ { as} f (s)$. Discuss how to apply the second shifting theorem to find the laplace transform of a delayed function. to apply the second shifting theorem for finding the laplace transform of a delayed function, first identify the original function and its delay parameter. Our expert help has broken down your problem into an easy to learn solution you can count on. question: 2. You'll need to complete a few actions and gain 15 reputation points before being able to upvote. upvoting indicates when questions and answers are useful. what's reputation and how do i get it? instead, you can save this post to reference later.

Step into a realm of endless possibilities as we unravel the mysteries of Solved Theorem 8 4 2 Second Shifting Theorem If Aoen0 And Chegg. Our blog is dedicated to shedding light on the intricacies, innovations, and breakthroughs within Solved Theorem 8 4 2 Second Shifting Theorem If Aoen0 And Chegg. From insightful analyses to practical tips, we aim to equip you with the knowledge and tools to navigate the ever-evolving landscape of Solved Theorem 8 4 2 Second Shifting Theorem If Aoen0 And Chegg and harness its potential to create a meaningful impact.

Laplace Transform: Second Shifting Theorem

Laplace Transform: Second Shifting Theorem

Laplace Transform: Second Shifting Theorem #Second Shifting Theorem of Inverse Laplace Transformation #Change Of Scale Property Laplace Transform | Second Shifting Theorem | Concept & Example by GP Sir How to use second shifting theorem for solving problems? Laplace Transform of a Piecewise Function (Unit Step Function) The Second Translation Theorem for Laplace Transforms Second Shifting Theorem | Type 1 Problems | t Shift | Heaviside Theorem | Laplace transform | Maths Differential Equations Laplace Second Shifting Theorem Laplace second shifting theorem | second shifting theorem proof | 2nd Shifting theorem Inverse Laplace transform of Second Shifting Theorem in English SECOND SHIFTING THEOREM | LAPLACE TRANSFORM | WITH SOLVED PROBLEMS | Second shifting theorem of Laplace transforms Laplace & Inverse Laplace Transform - Second Shifting Theorem | GP Sir Second Shifting Property in Laplace Transform | Second Shifting Theorem | Examples and Solutions Second Shifting Theorem of Laplace Transform with examples|| #laplace Second shifting theorem: Laplace transforms Laplace Transforms | Lecture 17 | Second Shifting Theorem Differential : Second Shifting Theorem Laplace Transform-7 Second Shifting Theorem and Change Of Scale Properly of Laplace Transforms | Lecture-8

Conclusion

After exploring the topic in depth, there is no doubt that the post offers useful wisdom about Solved Theorem 8 4 2 Second Shifting Theorem If Aoen0 And Chegg. All the way through, the scribe exhibits considerable expertise on the subject. Markedly, the chapter on important characteristics stands out as a crucial point. The narrative skillfully examines how these factors influence each other to form a complete picture of Solved Theorem 8 4 2 Second Shifting Theorem If Aoen0 And Chegg.

Furthermore, the piece is noteworthy in explaining complex concepts in an straightforward manner. This comprehensibility makes the explanation beneficial regardless of prior expertise. The analyst further augments the presentation by embedding related scenarios and tangible use cases that help contextualize the abstract ideas.

Another facet that makes this post stand out is the comprehensive analysis of various perspectives related to Solved Theorem 8 4 2 Second Shifting Theorem If Aoen0 And Chegg. By analyzing these diverse angles, the piece provides a well-rounded picture of the topic. The completeness with which the writer tackles the theme is highly praiseworthy and establishes a benchmark for comparable publications in this discipline.

Wrapping up, this write-up not only informs the observer about Solved Theorem 8 4 2 Second Shifting Theorem If Aoen0 And Chegg, but also inspires deeper analysis into this fascinating field. Whether you are just starting out or a seasoned expert, you will come across useful content in this exhaustive article. Many thanks for reading this detailed write-up. If you have any questions, please feel free to get in touch by means of the comments section below. I am excited about your thoughts. To expand your knowledge, here is a number of associated posts that are interesting and supplementary to this material. May you find them engaging!