Solved The Empty Set And Only The Empty Set Has Chegg

Solved Question Chegg Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. see answer. 1.the empty set is a proper subset of every set. 2.the empty set, and only the empty set, has cardinality zero. 3.the empty set has no subsets. 4.for any universal set, the complement of the empty set is nonempty. 5.a union with the empty set is always empty. 6.the power set of the empty set is empty. 7.the empty set is a subset of every set.

Solved The Empty Set And Only The Empty Set Has Chegg Another way to see at this is by looking at the number of elements in the sets: by definition, the empty set has zero elements, while the set containing the empty set has one element. A set that does not contain any element is called an empty set or a null set. an empty set is denoted using the symbol '∅'.learn about empty sets, their definition, and properties with solved examples. In this article, we have learned about the empty set, its properties and representation. let’s solve some examples and practice problems to understand the concept better. Answer ) a one reason power set of a given set (let a), is the set containing all subsets of that set (i.e. all subsets of set a). note : power set contains the empty and the set itself.
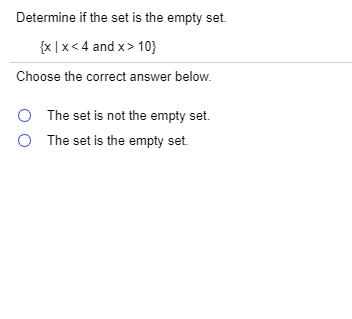
Solved Determine If The Set Is The Empty Set X X In this article, we have learned about the empty set, its properties and representation. let’s solve some examples and practice problems to understand the concept better. Answer ) a one reason power set of a given set (let a), is the set containing all subsets of that set (i.e. all subsets of set a). note : power set contains the empty and the set itself. Question: 1a. prove the empty set is a bijection from the empty set to the empty set. b. that ∅ is a relation, i.e., a set of ordered pairs. (so you have to prove that every member of ∅ is an ordered pair.) c. that ∅ is in fact a function. Step 1 statement: if a is a finite subset of r, then the derived set a ′ of a is empty, i.e. a ′ = ϕ (the empty set). Mark all statements that are correct. the empty set, and only the empty set, has cardinality zero. the power set of the empty set is empty. the cartesian product a cross times b is empty if a is empty or b is empty. the empty set is a subset of every set. the empty set is a proper subset of every set. The last line seems to be a form of the statement that "the empty set" is unique. the proof you presented shows that any two arbitrarily given empty sets are equal.

Solved Determine If The Set Is The Empty Set X X Question: 1a. prove the empty set is a bijection from the empty set to the empty set. b. that ∅ is a relation, i.e., a set of ordered pairs. (so you have to prove that every member of ∅ is an ordered pair.) c. that ∅ is in fact a function. Step 1 statement: if a is a finite subset of r, then the derived set a ′ of a is empty, i.e. a ′ = ϕ (the empty set). Mark all statements that are correct. the empty set, and only the empty set, has cardinality zero. the power set of the empty set is empty. the cartesian product a cross times b is empty if a is empty or b is empty. the empty set is a subset of every set. the empty set is a proper subset of every set. The last line seems to be a form of the statement that "the empty set" is unique. the proof you presented shows that any two arbitrarily given empty sets are equal.

Solved Consider The Empty Set ø And The Set Containing The Chegg Mark all statements that are correct. the empty set, and only the empty set, has cardinality zero. the power set of the empty set is empty. the cartesian product a cross times b is empty if a is empty or b is empty. the empty set is a subset of every set. the empty set is a proper subset of every set. The last line seems to be a form of the statement that "the empty set" is unique. the proof you presented shows that any two arbitrarily given empty sets are equal.
Comments are closed.