Solved Solve The Given Optimization Problem By Using Chegg Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. see answer. In this section we will use a general method, called the lagrange multiplier method, for solving constrained optimization problems:.
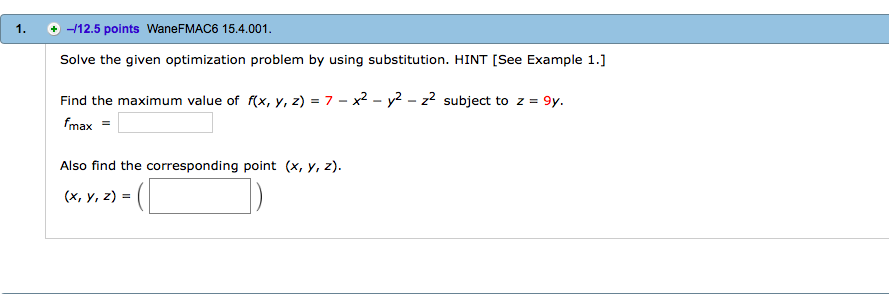
Solved Solve The Given Optimization Problem By Using Chegg In manufacturing, it is often desirable to minimize the amount of material used to package a product with a certain volume. in this section, we show how to set up these types of minimization and maximization problems and solve them by using the tools developed in this chapter. Create and solve an optimization problem using named index variables. the problem is to maximize the profit weighted flow of fruit to various airports, subject to constraints on the weighted flows. Example. consider the constrained optimization problem minimize 2 2 subject to x 1 2x1x2 3x 2 4x1 5x2 6x3 x1 2x2 = 3. Identify the constraints. if your objective function has more than one variable, you will need to use one or more constraints in the problem to write equations that relate the variables together.
Solved Solve The Given Optimization Problem By Using Chegg Example. consider the constrained optimization problem minimize 2 2 subject to x 1 2x1x2 3x 2 4x1 5x2 6x3 x1 2x2 = 3. Identify the constraints. if your objective function has more than one variable, you will need to use one or more constraints in the problem to write equations that relate the variables together. Now we demonstrate how to use excel spreadsheet modeling and solver to find the optimal solution of optimization problems. if the model has two variables, the graphical method can be used to solve the model. very few real world problems involve only two variables. There are many available solvers for this class of problems. in lieu of a linearly constrained linear least squares solver, this can be solved with any quadratic programming solver, because a linearly constrained linear least squares problem is a convex quadratic programming (qp) problem. We begin from reviewing optimization methods applied for solving static optimization problems in sdm networks, afterwards, we focus on algorithmic approaches for dynamic resource allocation problems in such networks. Defining an optimization problem suppose, we are to design an optimal pointer made of some material with density ρ. the pointer should be as low weight as possible, with a desirable strength (i.e. sustainable to mechanical breakage) and the deflection of pointing at end should be negligible.
Comments are closed.