Solved Show Prove That For Any Integer %d1%80%d1%9c %d0%b2 %d1%95 1 And Any Chegg

Prove That For Every Positive Integer D There Is An Chegg There are 2 steps to solve this one. "for any integer n ≥ 1 , ∑ j = 1 n (2 j 1) = n (n 2) ." use induction to prove that for any integer n≥1,∑j=1n (2j 1)=n(n 2). Induction is an axiom which allows us to prove that certain properties are true for all positive integers (or for all nonnegative integers, or all integers >= some fixed number).

Solved 1 Prove That For Any Integer A One Of The Integers Chegg We will prove the statement by mathematical induction. let p (n) be the inequality 2^n < (n 2)!. we will show that p (n) is true for every integer n ≥ 0. show that p (0) is true:. We have to show that, given this assumption, the statement is also true for k 1. we need to evaluate ∑i=1 to k 1 of i i!. by the inductive hypothesis, we know that ∑i=1 to k of i i! = (k 1)! 1. now we only need to add the term for k 1: (k 1) (k 1)! = (k 1)! k!. Use strong mathematical induction to prove that for any integer n ≥ 2, if n is even, then any sum of n odd integers is even, and if n is odd, then any sum of n odd integers is odd. Use proof by induction to show that for any positive integer $n\geq 2$ the following holds: $ (1 \frac {1} {3}) (1 \frac {1} {5}) (1 \frac {1} {2n 1})>\frac {\sqrt {2n 1}} {3}$ proof: base case: $n=2$. $.

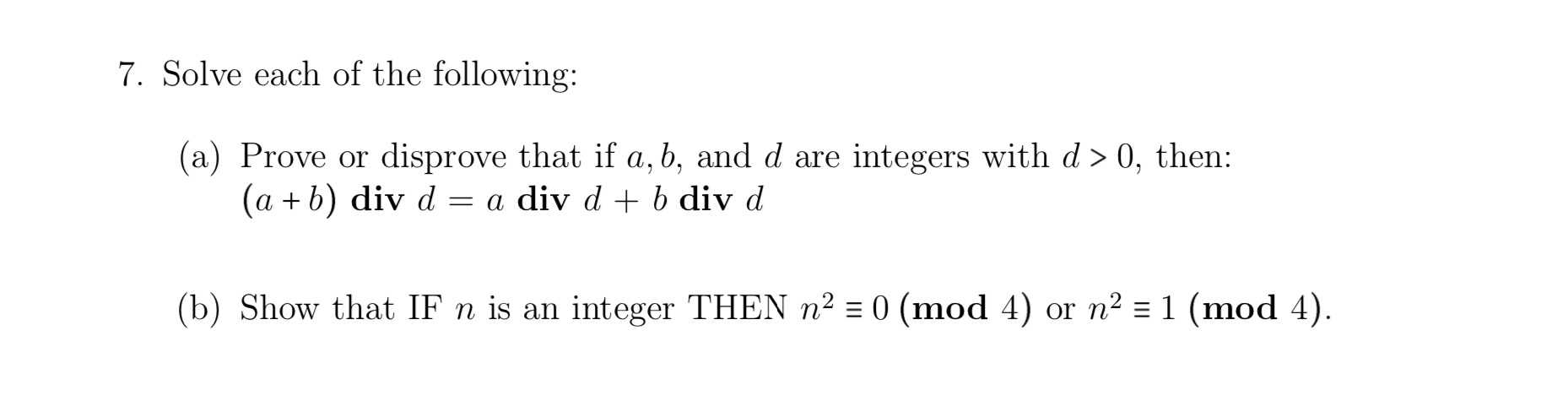
Solve Each Of The Following A ï Prove Or Disprove Chegg Use strong mathematical induction to prove that for any integer n ≥ 2, if n is even, then any sum of n odd integers is even, and if n is odd, then any sum of n odd integers is odd. Use proof by induction to show that for any positive integer $n\geq 2$ the following holds: $ (1 \frac {1} {3}) (1 \frac {1} {5}) (1 \frac {1} {2n 1})>\frac {\sqrt {2n 1}} {3}$ proof: base case: $n=2$. $. Mathematical induction attempts to establish that a given statement is true for all natural numbers by direct proof in two steps: the base case proves the given statement for the first natural number. Study with quizlet and memorize flashcards containing terms like principle of mathematical induction, general structure of proofs by induction, strong induction and more. B.it is claimed that for each integer n ≥ 0, the nth term of the sequence has the same value as that given by the formula 2 · 5n 1. in other words, the claim is that the terms of the sequence satisfy the equation an = 2 · 5n 1. prove that this is true. a. a1 = 2. a4 = 5a4 1 = 5a3 = 5 · 50 = 250. Math advanced math advanced math questions and answers 1. prove that for any integer a, a (a 1) (a 2) is divisible by 3.