Solved Question 1 1 3 Points Consider The Relation R Chegg

Solved Question 2 Consider The Following Relations Chegg Step 1 to normalize the given relation r into 3nf (third normal form), we need to follow these steps: 1) ide. To decompose r into 2nf, let's break down r into smaller relations so that no partial dependencies exist. this may result in relations like: r1 (a, d, e), r2 (a, b, c), r3 (b, f), and r4 (f, g, h), r5 (d, i, j).

Solved Question 2 Consider The Following Relations Chegg Now, let's identify the normal form that r satisfies. r satisfies the third normal form (3nf) because all non prime attributes are fully functionally dependent on the candidate keys. Consider a relation r (a, b, c, d, e, f, g, h), where each attribute is atomic, and following functional dependencies exist. the relation r is . the correct answer is option 1. explanation: since attribute d is not a part of any fd, it must be a part of the candidate key. ad = {abcdefgh} bd = {abcdefgh} ed = {abcdefgh} fd = {abcdefgh}. Step 1 to determine whether the given relation r is in 1nf, 2nf, and 3nf, let's analyze each of these norma. Usewarshall's algorithm to find the transitive closure of r by performing the following two steps: (a) computer the matrices w0,w1,w2,w3,w4 and w5. (b) find (all the ordered pairs of) the transitive closure of r. here’s the best way to solve it.

Solved Question 1 1 3 Points Consider The Relation R Chegg Step 1 to determine whether the given relation r is in 1nf, 2nf, and 3nf, let's analyze each of these norma. Usewarshall's algorithm to find the transitive closure of r by performing the following two steps: (a) computer the matrices w0,w1,w2,w3,w4 and w5. (b) find (all the ordered pairs of) the transitive closure of r. here’s the best way to solve it. Identify and explain any two (2) algorithms that could be used to solve the problem. b.) explain the time complexity of the chosen algorithms (best case worst case). use the time complexity measures to explain the suitability of the algorithms to solve a given problem. Now we decompose relation r into three new relations r1, r2 and r3 that are all in 2nf. the primary key of relation r1 is {a ‾ \textit {\underline {a}} a , b ‾ \textit {\underline {b}} b }, of relation r2 is a ‾ \textit {\underline {a}} a and of r3 is b ‾ \textit {\underline {b}} b . A consider the universal relation r = {a, b, c, d, e, f, g, h, i, j} and the set of functional dependencies f = { {a, b} > {c}, {b, d} > {e, f}, {a, d} > {g, h}, {a} > {i}, {h} > {j}}. Consider the set of fd: ab→cd and c→d. since ab → cd implies ab → abcd. it is a primary key since there are no smaller ubsets of keys that hold over r(a,b,c,d). the fd d ∈ c is false; that is, it is not a trivial fd c is not a superkey d is not part of some key for r.
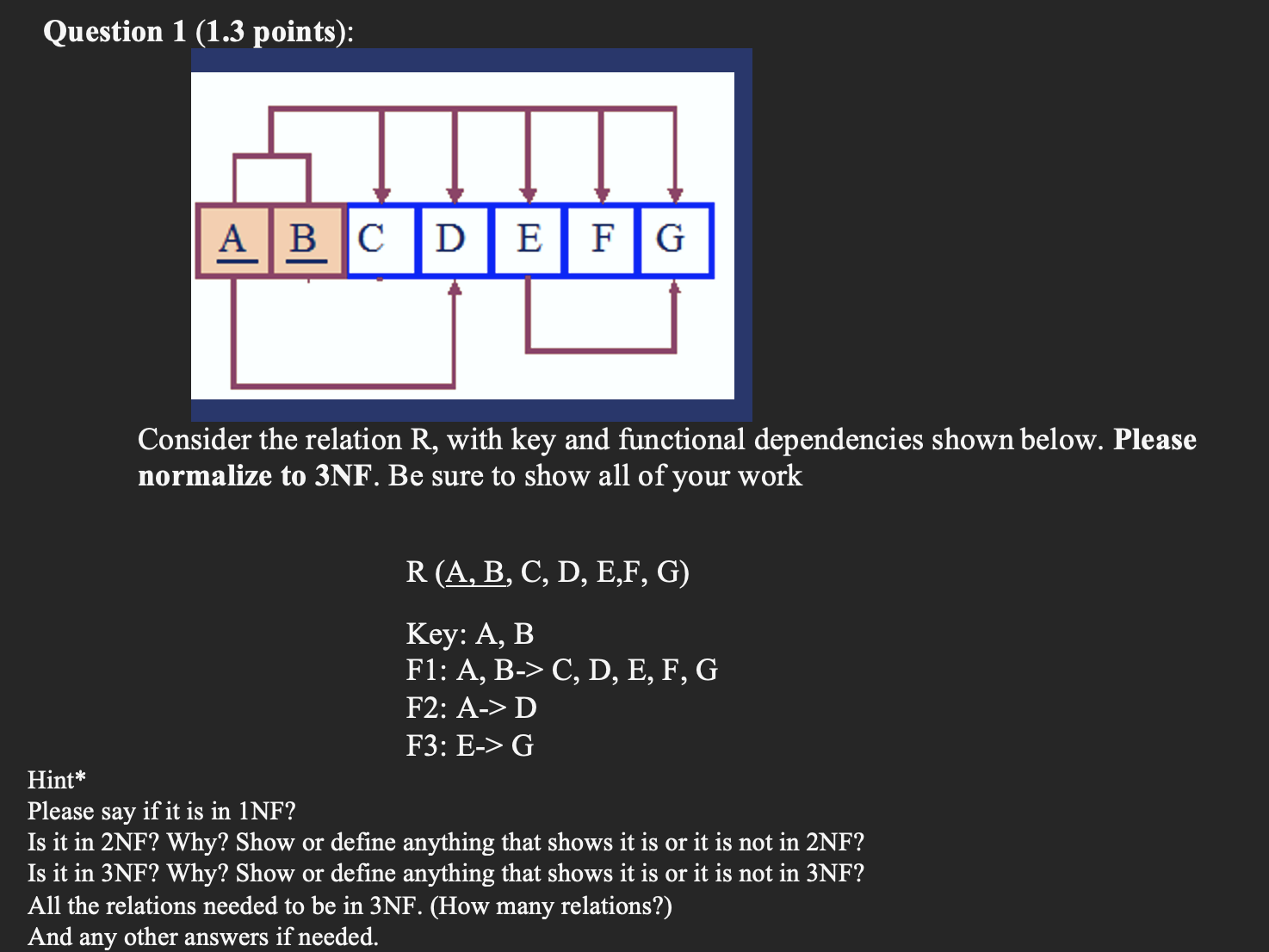
Solved Question 1 1 3 Points Consider The Relation R Chegg Identify and explain any two (2) algorithms that could be used to solve the problem. b.) explain the time complexity of the chosen algorithms (best case worst case). use the time complexity measures to explain the suitability of the algorithms to solve a given problem. Now we decompose relation r into three new relations r1, r2 and r3 that are all in 2nf. the primary key of relation r1 is {a ‾ \textit {\underline {a}} a , b ‾ \textit {\underline {b}} b }, of relation r2 is a ‾ \textit {\underline {a}} a and of r3 is b ‾ \textit {\underline {b}} b . A consider the universal relation r = {a, b, c, d, e, f, g, h, i, j} and the set of functional dependencies f = { {a, b} > {c}, {b, d} > {e, f}, {a, d} > {g, h}, {a} > {i}, {h} > {j}}. Consider the set of fd: ab→cd and c→d. since ab → cd implies ab → abcd. it is a primary key since there are no smaller ubsets of keys that hold over r(a,b,c,d). the fd d ∈ c is false; that is, it is not a trivial fd c is not a superkey d is not part of some key for r.

Solved Prev Consider The Following Relation S 3 4 Chegg A consider the universal relation r = {a, b, c, d, e, f, g, h, i, j} and the set of functional dependencies f = { {a, b} > {c}, {b, d} > {e, f}, {a, d} > {g, h}, {a} > {i}, {h} > {j}}. Consider the set of fd: ab→cd and c→d. since ab → cd implies ab → abcd. it is a primary key since there are no smaller ubsets of keys that hold over r(a,b,c,d). the fd d ∈ c is false; that is, it is not a trivial fd c is not a superkey d is not part of some key for r.
Comments are closed.