Solved Q2 Prove Or Disprove The Expressions Below Using Chegg

Solved Q2 Prove Or Disprove The Expressions Below Using Chegg Q2. prove or disprove the expressions below using truth tables. include a sentence explaining if it is proven or disproven and why. ( 30 points) a) (a⋅c) b =(a b)⋅c (15 points) b) (a b)⋅c =(c ⋅a) (b⋅c) (15 points). Using the inference rules above, we can solve the following riddle by first formalizing the text into propositional logic and then using the inference rules to find the glasses.

Solved Prove Or Disprove The Following Expressions A Chegg Prove or disprove the expressions below using truth tables. include a sentence explaining if it is proven or disproven and why. (30 points) a) (15 points) each of the rows for the expressions above matche; therefore, the expression is proven to be true. Prove or disprove below: if a is a regular language, then there is a number p (the pumping length) where, if s is any string in a of length at least p, then s may be divided into 3 pieces, s = xyz, satisfying the 3 pumping lemma conditions. Use de morgan's laws to find the negation of the given statement. the negation of the statement "james is young and strong" using de morgan's law is "james is not young, or he is not strong.". To prove the equivalence of two regular expressions , we should try to reduce one r.e. into r.e using identities which we have or using proper reductions.for understanding proper reduction , let us understand by a simple example first :.
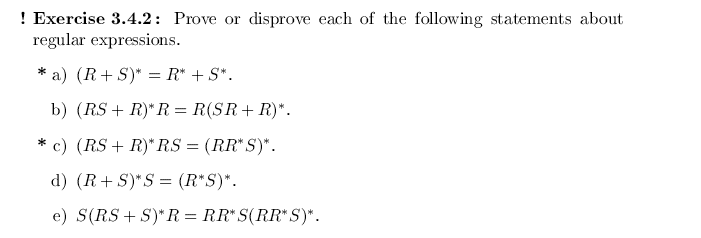
Solved Exercise 3 4 2 Prove Or Disprove Each Of The Chegg Use de morgan's laws to find the negation of the given statement. the negation of the statement "james is young and strong" using de morgan's law is "james is not young, or he is not strong.". To prove the equivalence of two regular expressions , we should try to reduce one r.e. into r.e using identities which we have or using proper reductions.for understanding proper reduction , let us understand by a simple example first :. Our expert help has broken down your problem into an easy to learn solution you can count on. question: exercise 3.4.2: prove or disprove each of the following statements about regular expressions. * a) (r s)* = r* s* c) (rs r)*rs = (rrs)*: here’s the best way to solve it. Our expert help has broken down your problem into an easy to learn solution you can count on. here’s the best way to solve it. not the question you’re looking for? post any question and get expert help quickly. Search our library of 100m curated solutions that break down your toughest questions. ask one of our real, verified subject matter experts for extra support on complex concepts. test your knowledge anytime with practice questions. create flashcards from your questions to quiz yourself. Ask any question and get an answer from our subject experts in as little as 2 hours.

Solved Q2 Prove Or Disprove The Following Using Truth Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. question: exercise 3.4.2: prove or disprove each of the following statements about regular expressions. * a) (r s)* = r* s* c) (rs r)*rs = (rrs)*: here’s the best way to solve it. Our expert help has broken down your problem into an easy to learn solution you can count on. here’s the best way to solve it. not the question you’re looking for? post any question and get expert help quickly. Search our library of 100m curated solutions that break down your toughest questions. ask one of our real, verified subject matter experts for extra support on complex concepts. test your knowledge anytime with practice questions. create flashcards from your questions to quiz yourself. Ask any question and get an answer from our subject experts in as little as 2 hours.

Solved Q2 Prove Or Disprove The Following Using Truth Chegg Search our library of 100m curated solutions that break down your toughest questions. ask one of our real, verified subject matter experts for extra support on complex concepts. test your knowledge anytime with practice questions. create flashcards from your questions to quiz yourself. Ask any question and get an answer from our subject experts in as little as 2 hours.
Comments are closed.