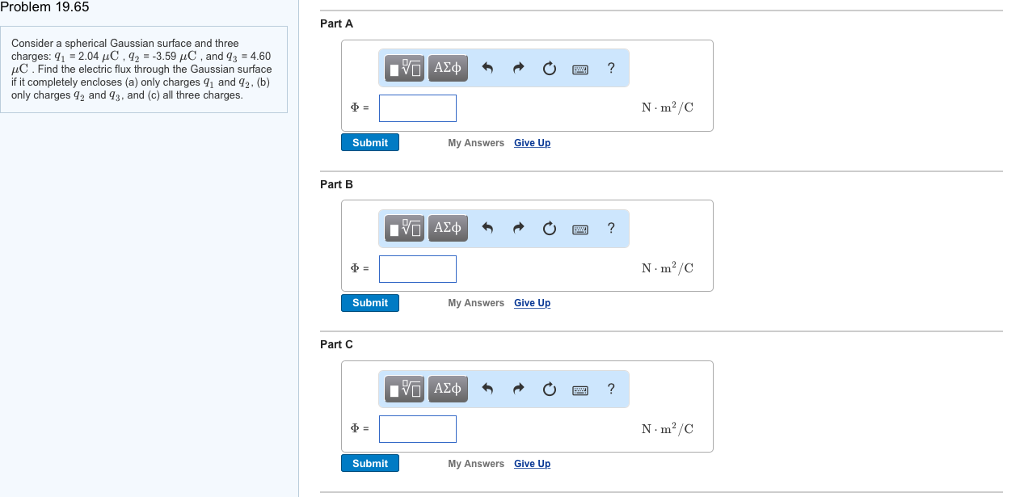
Solved Problem 19 65 Consider A Spherical Gaussian Surface Chegg Problem 19.65 consider a spherical gaussian surface and three charges: q1 = 2.01 μc , q2 = 3.29 μc , and q3 = 4.62 μc . find the electric flux through the gaussian surface if it completely encloses (a) only charges q1 and q2, (b) only charges q2 and q3, and (c) all three charges. Knowing this, we must divide the total charge on the outer surface by the sum of the length of each of the triangle’s sides in order to find the average linear charge density:.
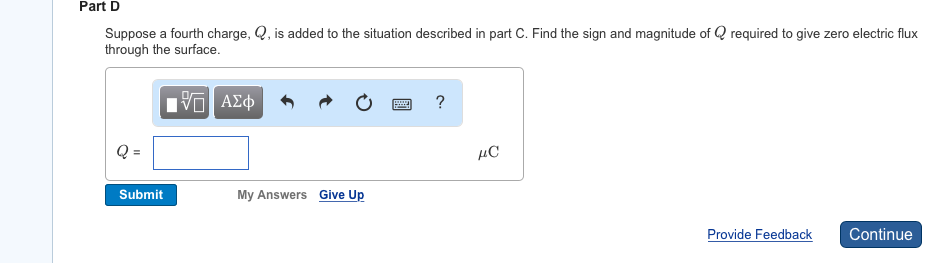
Solved Problem 19 65 Consider A Spherical Gaussian Surface Chegg Find the sign and magnitude of q required to give zero electric flux through the surface. i'm pretty sure that this problem involves the equation φ = q ε0, but have no idea on how to incorporate the given values into this problem. Imagine that the space is surrounded by a gaussian surface of the exact same dimension as the cube and that the e field caused by the charges is normal to the faces of the gaussian cube. Spherical gaussian surface of radius: solved problem, exercises for electrical engineering. Video answer: where should the charge be located in order to maximize the magnitude of the event? the charge enclosed by that surface and god's law determine the total flux through that closed….
Solved Problem 19 65 Consider A Spherical Gaussian Surface Chegg Spherical gaussian surface of radius: solved problem, exercises for electrical engineering. Video answer: where should the charge be located in order to maximize the magnitude of the event? the charge enclosed by that surface and god's law determine the total flux through that closed…. Note that the ring will have a flux through the surface, but all the flux that enter the surface through one side will leave leave from the other side and the net flux from the ring through the surface is zero. Determine the direction of the electric field, and a “gaussian surface” on which the magnitude of the electric field is constant over portions of the surface. To determine under what conditions the electric flux through the sides of a cube would be the same as through a spherical surface, we need to consider the relationship between the electric field and the surface area of each shape. To determine the position of a charge q placed inside a spherical gaussian surface of radius r that maximizes the electric flux through the surface, we can refer to gauss's law.
Comments are closed.