Solved Problem 1 Using Similarity Transformation Transform Chegg

Solved Problem 1 Using Similarity Transformation Transform Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. try focusing on one step at a time. you got this! not the question you’re looking for? post any question and get expert help quickly. There are an infinite number of basis that span r n, hence there are infinite representations for the same vector. consider for example r 2. the standard basis vectors are {[1 0], [0 1]}, but another basis are {[1 1], [0 1]}, and yet another are {[1 1], [0 1]}, and so on.

Solved Problem 1 Using Similarity Transformation Transform Chegg Since the characteristic equation is of second order we don't even need to solve it in order to check that it has two distinct solutions. just check the discriminant instead. Our strategy now, which we will pursue in detail next time, is to use similarity transforms based on a to make a perturbed matrix a e look “almost” diagonal, and then use gershgorin theory to turn that “almost” diagonality into bounds on where the eigenvalues can be. Opencvs similarity transform is cv::estimaterigidtransform which allows you to compute a 4 degree of freedom (similarity transform) or 6 degree of freedom (full affine) transformation, depending on the parameters you choose. In the transfer function, there are six constraints. in state space, there are 16 degrees of freedom. what this means is there are in infinite number of ways to represent the same system in state space form. some of these forms have names. controller canonical form also has some of the worst numerical properties.

Winter0708 Similarity Transform Pdf Opencvs similarity transform is cv::estimaterigidtransform which allows you to compute a 4 degree of freedom (similarity transform) or 6 degree of freedom (full affine) transformation, depending on the parameters you choose. In the transfer function, there are six constraints. in state space, there are 16 degrees of freedom. what this means is there are in infinite number of ways to represent the same system in state space form. some of these forms have names. controller canonical form also has some of the worst numerical properties. Essential ideas dilation is a transformation that enlarges or reduces a pre image to create a similar image. the center of dilation is a fixed point at which the igure is either enlarged or reduced. A transformation $a$ to $sas^ { 1}$, for some invertible matrix $s$, is called a similarity transformation or conjugation of the matrix $a$. we say that matrices $a$ and $b$ are similar if there exists an invertible matrix $s$ such that $b=sas^ { 1}$. Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. see answer. To transform the given system into observable canonical form, find a similarity transformation matrix t such that the new state vector z (t) = t x (t), makes the matrix a ′ of the transformed system have an observable canonical structure, a ′ = [a 11 a 12 0 a 22].
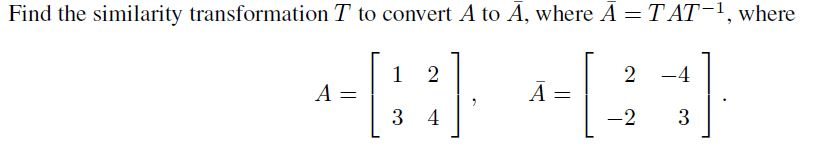
Solved Find The Similarity Transformation T To Convert A To Chegg Essential ideas dilation is a transformation that enlarges or reduces a pre image to create a similar image. the center of dilation is a fixed point at which the igure is either enlarged or reduced. A transformation $a$ to $sas^ { 1}$, for some invertible matrix $s$, is called a similarity transformation or conjugation of the matrix $a$. we say that matrices $a$ and $b$ are similar if there exists an invertible matrix $s$ such that $b=sas^ { 1}$. Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. see answer. To transform the given system into observable canonical form, find a similarity transformation matrix t such that the new state vector z (t) = t x (t), makes the matrix a ′ of the transformed system have an observable canonical structure, a ′ = [a 11 a 12 0 a 22].
Comments are closed.