Solved Problem 1 10 Points Approximating Pi The Value Of Chegg

Solved Problem 1 10 Points Approximating Pi The Value Of Chegg The number π is an irrational number and there are many differont methods to approximate its value. one approach to approximate π is from an infinite product, which is the product of infinitely many terms in a sequence. The idea is to simulate random (x, y) points in a 2 d plane with domain as a square of side 2r units centered on (0,0). imagine a circle inside the same domain with same radius r and inscribed into the square.

Solved Problem 1 10 Points Approximating Pi The Value Of Chegg You are supposed to use the described algorithm to approximate π, not use the built in value in python. i'd really appreciate it if someone could help me understand what the problem is asking, since i've read it so many times but still can't fully understand what it's saying. Make sure to use a while loop to solve the problem. use mathab and don't use the other chegg question, they are wrong. (approximating Ï€) a classic method of approximating the value of pi is to relate the area inside a circle to the area of a square just encompassing it. The orange line represents the actual value of pi, and the blue line is our approximation. you can see that it deviates a lot at the start, but very quickly falls down to near the actual. "π" (or pi) is the the ratio between the diameter and circumference of a circle. it's value is about 3.14, but accurately, it has an infinite amount of decimal places. this approximation of π is possible because if a regular polygon has more sides, it becomes more like a circle.

Solved 2 Problem 2 Approximating The Value Of π We Will Chegg The orange line represents the actual value of pi, and the blue line is our approximation. you can see that it deviates a lot at the start, but very quickly falls down to near the actual. "π" (or pi) is the the ratio between the diameter and circumference of a circle. it's value is about 3.14, but accurately, it has an infinite amount of decimal places. this approximation of π is possible because if a regular polygon has more sides, it becomes more like a circle. The greek mathematician archimedes used a fairly simple geometrical approach to estimate pi. see how he did it. Write a c function that calculates the value of π with a variable level of accuracy. for instance, if the desired accuracy is 10−6, the absolute difference between the true value of π (see below) and the approximation from your function is less than 10−6. Write a bot to make confident sounding statements about the value of pi with a random initial seed, then update with the median value of the digit sequences people post in response. There are two obvious issues that need to be solved but if you stare at them for 10 seconds, it is easy to see the solution. first, coin flips generate discrete numbers. second, they generate one dimensional numbers.
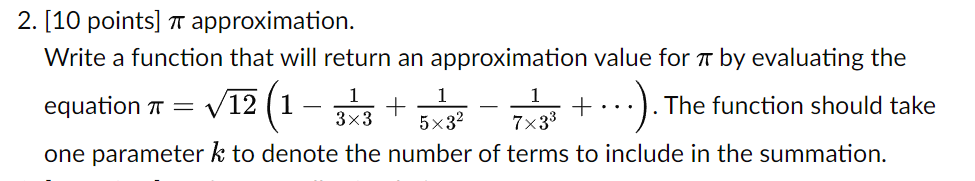
Solved 10 Points π Approximation Write A Function That Chegg The greek mathematician archimedes used a fairly simple geometrical approach to estimate pi. see how he did it. Write a c function that calculates the value of π with a variable level of accuracy. for instance, if the desired accuracy is 10−6, the absolute difference between the true value of π (see below) and the approximation from your function is less than 10−6. Write a bot to make confident sounding statements about the value of pi with a random initial seed, then update with the median value of the digit sequences people post in response. There are two obvious issues that need to be solved but if you stare at them for 10 seconds, it is easy to see the solution. first, coin flips generate discrete numbers. second, they generate one dimensional numbers.

Solved Exercise 1 50 Points Approximating π In This Chegg Write a bot to make confident sounding statements about the value of pi with a random initial seed, then update with the median value of the digit sequences people post in response. There are two obvious issues that need to be solved but if you stare at them for 10 seconds, it is easy to see the solution. first, coin flips generate discrete numbers. second, they generate one dimensional numbers.
Comments are closed.