Solved Practice 3 Finding An Inverse Function A Write An Chegg

Solved Practice 3 Finding An Inverse Function A Write An Chegg Question: practice 3. finding an inverse function a) write an equation for the inverse function for the one to one function defined by f (x)=x−12x b) the function f is one to one. Here is a set of practice problems to accompany the inverse functions section of the graphing and functions chapter of the notes for paul dawkins algebra course at lamar university.

Solved C Finding The Inverse Of A Function 10 Work Out Chegg To find the inverse of a function, solve the "y=" equation for x. then swap the variables. the result is the inverse of the original function. Inverse functions an inverse function goes the other way! let us start with an example: here we have the function f (x) = 2x 3, written as a flow diagram: the inverse function goes the other way: so the inverse of: 2x 3 is: (y−3) 2 the inverse is usually shown by putting a little " 1" after the function name, like this: f 1(y) we say "f. Tutorial on how to find the inverse of a function including several examples with detailed solutions. Free inverse function calculator step by step solutions to help find the inverse of the function.

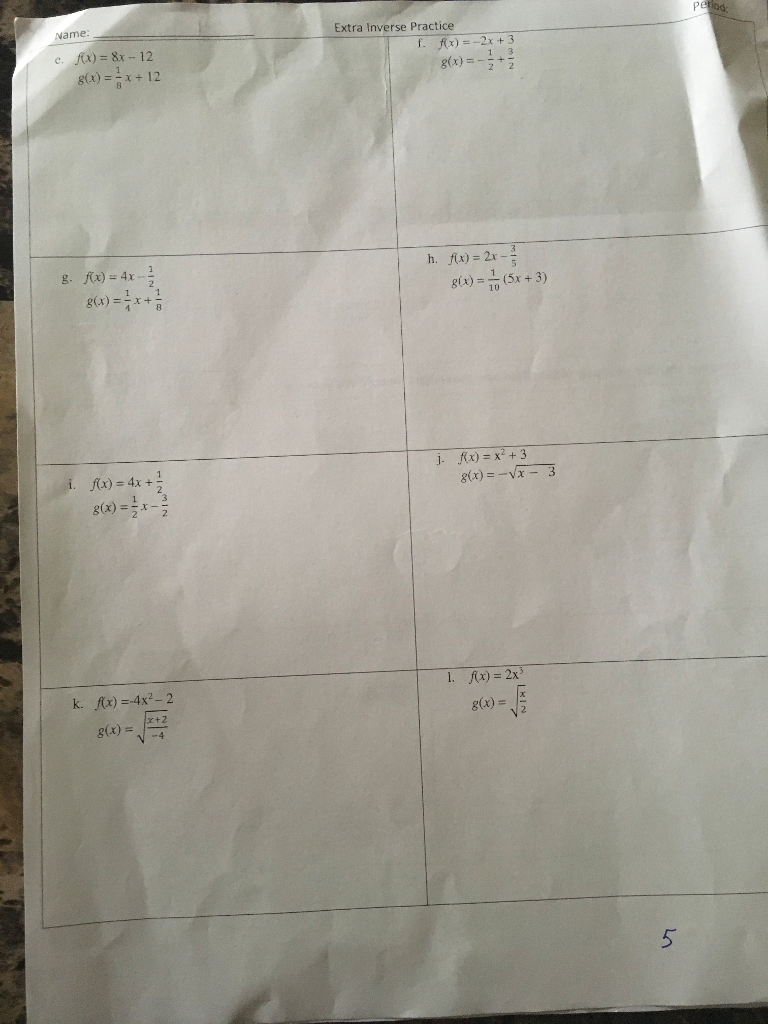
Solved Extra Inverse Practice Find The Inverse Of Each Chegg Tutorial on how to find the inverse of a function including several examples with detailed solutions. Free inverse function calculator step by step solutions to help find the inverse of the function. State if the given functions are inverses. find the inverse of each functions. We will look at an overview of inverse functions along with the process used to find the inverse of a function. in addition, we will see several examples with answers to understand the application of this process. If (3,5) is a point on the graph of y = f (x), a one to one function, and f' (3) = 2, then which of the following must be true? a. [f ¹ (3)] = 1 2 c. [ ¹ (5)]= = 2. 5) how do you find the inverse of a function algebraically? 1. each output of a function must have exactly one output for the function to be one to one. if any horizontal line crosses the graph of a function more than once, that means that \ (y\) values repeat and the function is not one to one.