Solved Module 5 Discrete Fourier Transform Dft And The Chegg
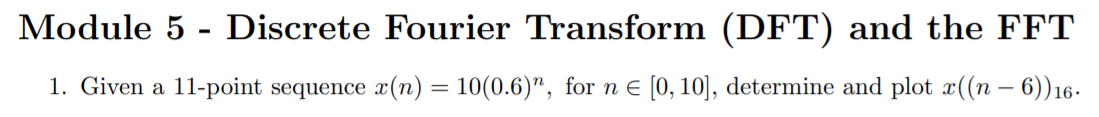
Solved Module 5 Discrete Fourier Transform Dft And The Chegg Write a function y = circconv (x1, x2, n) to implement circular convolution (in the discrete time domain), where, 2į and x2 are the input sequences of lengths l1, l2; such that l1, l2 < n. The discrete fourier transform, or dft, is the primary tool of digital signal processing. the foundation of the product is the fast fourier transform (fft), a method for computing the dft with reduced execution time.

Solved Question 3 The Discrete Fourier Transform Dft And Chegg The point: a brief review of the relevant review of fourier series; introduction to the dft and its good properties (spectral accuracy) and potential issues (aliasing, error from lack of smoothness). We can see that, lhs = rhs. (hence proved). One function should use the dft (fft in matlab), the other function should compute the circular convolution directly not using the dft. verify that both matlab functions give the same results. Question: module 5 discrete fourier transform (dft) and the fft 1. given a 11 point sequence x (n) = 10 (0.6)”, for n € [0, 10), determine and plot x ( (n – 6))16. solve by using matlab. please also provide the solution of matlab code.

Solved Question 4 How Is The Discrete Fourier Transform Chegg One function should use the dft (fft in matlab), the other function should compute the circular convolution directly not using the dft. verify that both matlab functions give the same results. Question: module 5 discrete fourier transform (dft) and the fft 1. given a 11 point sequence x (n) = 10 (0.6)”, for n € [0, 10), determine and plot x ( (n – 6))16. solve by using matlab. please also provide the solution of matlab code. Consider a complex discrete time signal x[n] with n samples with discrete fourier transform (dft) x[k]. (a) state the expression for x[k] in terms of x[n] and the number of real multiply operations to compute x[k]. Question 5: the discrete and fast fourier transform this question is concerned with the discrete fourier transform, and the fast fourier transform. answer all parts of this question. As we have n sampling points, it seems natural to compute n fourier coefficients c k (f) for the fourier series expansion of f (x). to compute the integrals for the fourier coefficients, we recall the definition of the composite trapezoidal rule to approximate integrals. In this section we will discuss the use of the fft to approximate the fourier transform of signals. recall that the dft and fft are discrete frequency domain representations of a discrete time sequence. in our examples, these sequences will be obtained by sampling continuous time signals.

Solved Question 3 The Discrete Fourier Transform Dft And Chegg Consider a complex discrete time signal x[n] with n samples with discrete fourier transform (dft) x[k]. (a) state the expression for x[k] in terms of x[n] and the number of real multiply operations to compute x[k]. Question 5: the discrete and fast fourier transform this question is concerned with the discrete fourier transform, and the fast fourier transform. answer all parts of this question. As we have n sampling points, it seems natural to compute n fourier coefficients c k (f) for the fourier series expansion of f (x). to compute the integrals for the fourier coefficients, we recall the definition of the composite trapezoidal rule to approximate integrals. In this section we will discuss the use of the fft to approximate the fourier transform of signals. recall that the dft and fft are discrete frequency domain representations of a discrete time sequence. in our examples, these sequences will be obtained by sampling continuous time signals.

Exercise 1 Discrete Fourier Transform The N Point Chegg As we have n sampling points, it seems natural to compute n fourier coefficients c k (f) for the fourier series expansion of f (x). to compute the integrals for the fourier coefficients, we recall the definition of the composite trapezoidal rule to approximate integrals. In this section we will discuss the use of the fft to approximate the fourier transform of signals. recall that the dft and fft are discrete frequency domain representations of a discrete time sequence. in our examples, these sequences will be obtained by sampling continuous time signals.
Comments are closed.