Solved Let A 5 9 B 1 0 And C 4 2 Prove That Abc Is Chegg

Solved Let C A B Aôëñb A Bôêê 0 1 Prove That â C B 0 1 Chegg We must show that u⋅v,u⋅w, or v⋅w is zero in order to show that one of these pairs is orthogonal. u⋅v = u⋅w= v⋅w= since bc ⊥ac, abc is a right angled triangle. Since the dot product of u and v is zero, we can conclude that u and v are perpendicular, and therefore, angle b is a right angle. thus, triangle abc is a right angled triangle.

Solved Let A 1 2 4 B 1 5 2 And C 5 0 1 A Chegg Note that we can also show that angle a or angle c is a right angle by calculating the dot product of other pairs of vectors. for example, we can calculate the dot product of vectors ( 6, 9) and (3, 2) to show that angle a is a right angle:. How does the proofs calculator work? this calculator has 1 input. what 2 formulas are used for the proofs calculator? build a bridge using corollaries, axioms, and theorems to get to the declarative statement. take the quiz. what 8 concepts are covered in the proofs calculator?. We must show that u⋅v,u⋅w, or v⋅w is zero in order to show that one of these pairs is orthogonal. u v=u⋅w=v w= here’s the best way to solve it. let a=(−5,9),b =(1,0), and c = (4,2). prove that abc is a right angled triangle. let u= ab,v =bc, and w =ac. To prove abc is a right angled triangle, we found the vectors ab, bc, and ac. calculating the dot product between vectors ab and bc yielded zero, indicating they are perpendicular, thus confirming that abc is a right angled triangle at point b.

Solved Let A 5 9 B 1 0 And C 4 2 Prove That Abc Is Chegg We must show that u⋅v,u⋅w, or v⋅w is zero in order to show that one of these pairs is orthogonal. u v=u⋅w=v w= here’s the best way to solve it. let a=(−5,9),b =(1,0), and c = (4,2). prove that abc is a right angled triangle. let u= ab,v =bc, and w =ac. To prove abc is a right angled triangle, we found the vectors ab, bc, and ac. calculating the dot product between vectors ab and bc yielded zero, indicating they are perpendicular, thus confirming that abc is a right angled triangle at point b. In order to prove that abc is a right angled triangle, we'll have to show that one of the vector pairs is orthogonal, meaning that their dot product is zero. Question: let a= (−5,9),b= (1,0), and c= (4,2). prove that abc is a right angled triangle. let u=ab,v=bc, and w=ac. In order to determine if triangle abc, with vertices a (1, 4), b ( 1, 2), and c ( 2, 5), is isosceles, we need to calculate the lengths of its sides ab, bc, and ac and then compare them. since ac = bc, the triangle is isosceles. therefore, triangle abc is isosceles because it has two equal sides. Well i was trying directly multiplying both sides by $ (a 3)^2 (b 3)^2 (c 3)^2$ but it's too lengthy and seemed complex so any better way to solve it ? you could try the standard substitution $a=x y,b=y z,c=z x$ to remove the condition $abc=1$ and get an equivalent inequality for all positive reals.
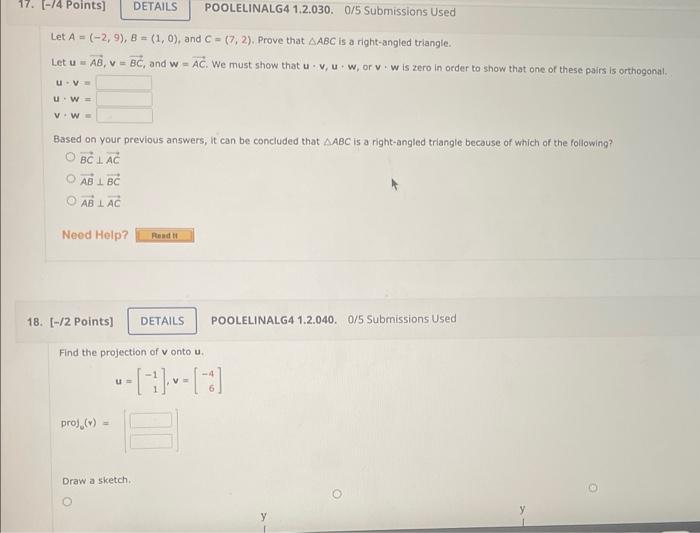
Solved Let A 2 9 B 1 0 And C 7 2 Prove That Abc Is Chegg In order to prove that abc is a right angled triangle, we'll have to show that one of the vector pairs is orthogonal, meaning that their dot product is zero. Question: let a= (−5,9),b= (1,0), and c= (4,2). prove that abc is a right angled triangle. let u=ab,v=bc, and w=ac. In order to determine if triangle abc, with vertices a (1, 4), b ( 1, 2), and c ( 2, 5), is isosceles, we need to calculate the lengths of its sides ab, bc, and ac and then compare them. since ac = bc, the triangle is isosceles. therefore, triangle abc is isosceles because it has two equal sides. Well i was trying directly multiplying both sides by $ (a 3)^2 (b 3)^2 (c 3)^2$ but it's too lengthy and seemed complex so any better way to solve it ? you could try the standard substitution $a=x y,b=y z,c=z x$ to remove the condition $abc=1$ and get an equivalent inequality for all positive reals.

Solved Homework 1 1 Let A 1 2 3 B 4 5 9 And C 9 1 1 Be Chegg In order to determine if triangle abc, with vertices a (1, 4), b ( 1, 2), and c ( 2, 5), is isosceles, we need to calculate the lengths of its sides ab, bc, and ac and then compare them. since ac = bc, the triangle is isosceles. therefore, triangle abc is isosceles because it has two equal sides. Well i was trying directly multiplying both sides by $ (a 3)^2 (b 3)^2 (c 3)^2$ but it's too lengthy and seemed complex so any better way to solve it ? you could try the standard substitution $a=x y,b=y z,c=z x$ to remove the condition $abc=1$ and get an equivalent inequality for all positive reals.
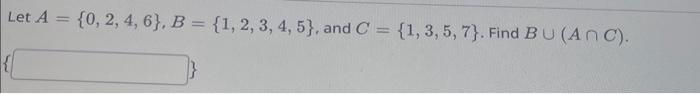
Solved Let A 0 2 4 6 B 1 2 3 4 5 And C 1 3 5 7 Find Chegg
Comments are closed.