Solved In Lecture We Derived The Following Solution To The Chegg

Solved In Lecture We Derived The Following Solution To The Chegg Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. see answer. In numerical analysis, the runge–kutta methods (english: ˈrʊŋəˈkʊtɑː ⓘ ruung ə kuut tah[1]) are a family of implicit and explicit iterative methods, which include the euler method, used in temporal discretization for the approximate solutions of simultaneous nonlinear equations. [2] these methods were developed around 1900 by the german mathematicians carl runge and wilhelm kutta.

Solved I Do Not Understand The Solution On Chegg Can Chegg As a first example showing how a diffusion problem may be solved analyti cally, we shall now derive the solution to an ideal but most important problem. the diffusion equation is a linear one, and a solution can, therefore, be obtained by adding several other solutions. In the lecture, we observed that the protein stability curve, as described by the derived expression, indicates that the native fold of proteins is only stable within a specific temperature window. To find the average dipole moment reduction factor, we need to calculate the value of cosh (a) sinh (a). the average dipole moment reduction factor is given by the expression cosh (a) sinh (a). By considering the fourier analysis equation or synthesis equation, show the validity in general of each of the following statements: if x(t) is real valued, then x(o) = x*( c).
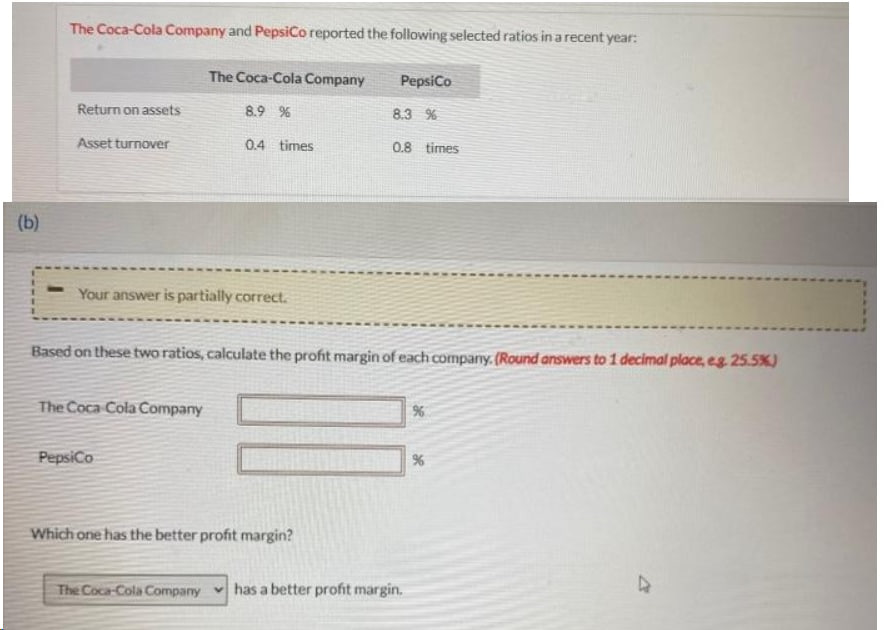
Solved Solved Chegg To find the average dipole moment reduction factor, we need to calculate the value of cosh (a) sinh (a). the average dipole moment reduction factor is given by the expression cosh (a) sinh (a). By considering the fourier analysis equation or synthesis equation, show the validity in general of each of the following statements: if x(t) is real valued, then x(o) = x*( c). Problem 2. in lectures, we derived the equation for the integrating factor for cases μ = μ (y) and μ = μ (x). a given differential equation may have integrating other than these two simple forms. a) try to find the equation of the integrating factor of the form μ = μ (x y). In lecture 1, we presented the full nonlinear surface water wave equations. in lecture 2, we considered the linear approximation to these equations in the case of flat bottom topography, but allowed for waves of any horizontal wavelength. Solve the following second order autonomous equations (“autonomous” is an im portant word; it means that the independent variable does not appear explicitly in the equation — it does lurk in the derivatives, of course.). Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. there are 2 steps to solve this one. not the question you’re looking for? post any question and get expert help quickly.
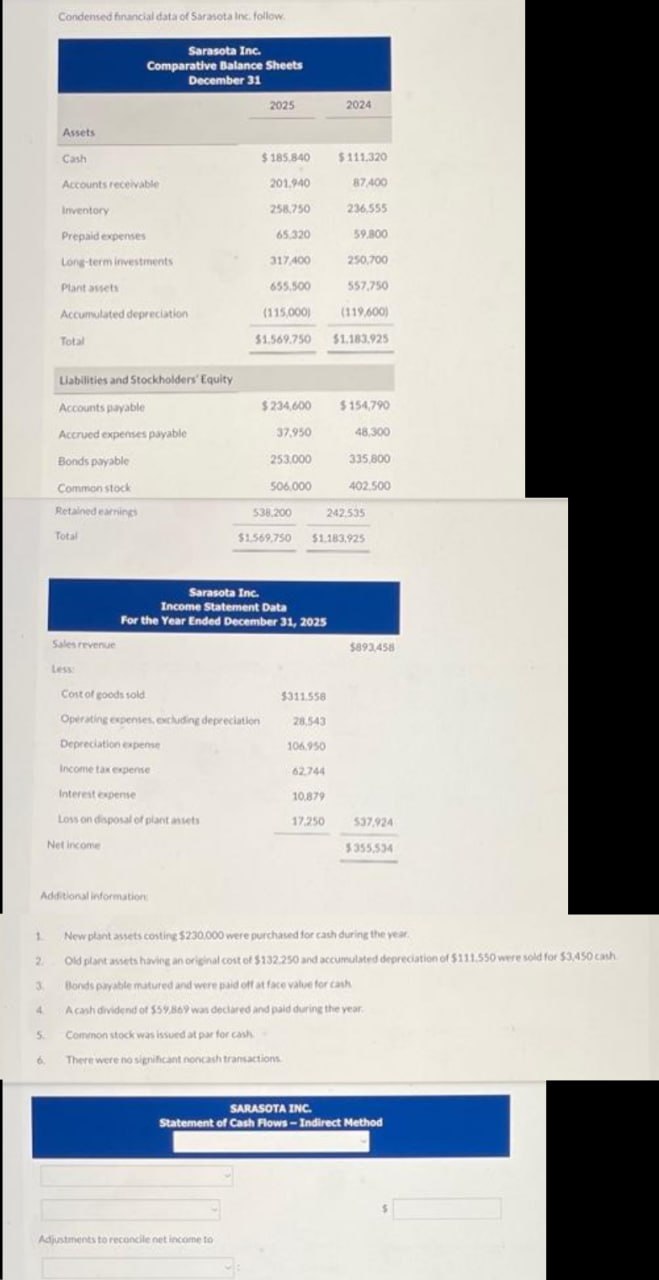
Solved Solved Chegg Problem 2. in lectures, we derived the equation for the integrating factor for cases μ = μ (y) and μ = μ (x). a given differential equation may have integrating other than these two simple forms. a) try to find the equation of the integrating factor of the form μ = μ (x y). In lecture 1, we presented the full nonlinear surface water wave equations. in lecture 2, we considered the linear approximation to these equations in the case of flat bottom topography, but allowed for waves of any horizontal wavelength. Solve the following second order autonomous equations (“autonomous” is an im portant word; it means that the independent variable does not appear explicitly in the equation — it does lurk in the derivatives, of course.). Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. there are 2 steps to solve this one. not the question you’re looking for? post any question and get expert help quickly.
Comments are closed.