Solved If A B C Is A Primitive Pythagorean Triple The Chegg
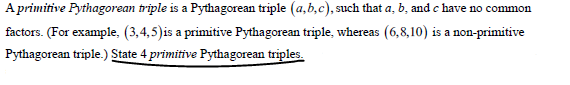
Solved A Primitive Pythagorean Triple Is A Pythagorean Chegg Question: if (a,b,c) is a primitive pythagorean triple, the number c is called the hypotenuse of the triple, for reasons that should be self explanatory. this exercise is meant to give some insight into what kinds of numbers can be the hypotenuse of a primitive pythagorean triple. Prove that if $a$, $b$, $c$ is a primitive pythagorean triple, $a$ and $b$ can't both be odd.

Solved In A Primitive Pythagorean Triple 8 22 Theorem If Chegg A primitive pythagorean triple is a pythagorean triple $a$,$b$,$c$ with the constraint that $\gcd (a,b)=1$, which implies $\gcd (a,c)=1$ and $\gcd (b,c)=1$. example: $a=3$,$b=4$,$c=5$ where, $9 16=25$. A primitive pythagorean triple, also known as reduced triple, is a set of positive integers (a, b, c) with a greatest common factor (gcf) of 1. primitive pythagorean triple will always have 1 even number and the value of c will always be odd. Some properties of primitive pythagorean triples: let a denote the odd leg, b denote the even leg, c denote the odd hypotenuse of a primitive pythagorean triple. If a, b, and c are relatively prime in pairs then (a, b, c) is a primitive pythagorean triple. clearly, if k divides any two of a, b, and c it divides all three.
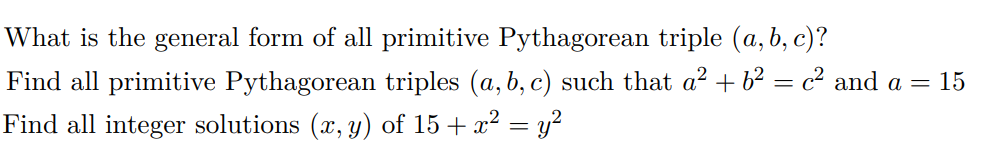
Solved What Is The General Form Of All Primitive Pythagorean Chegg Some properties of primitive pythagorean triples: let a denote the odd leg, b denote the even leg, c denote the odd hypotenuse of a primitive pythagorean triple. If a, b, and c are relatively prime in pairs then (a, b, c) is a primitive pythagorean triple. clearly, if k divides any two of a, b, and c it divides all three. If (a,b,c) is a primitive pythagorean triple, the number c is called the hypotenuse of the triple, for reasons that should be self explanatory. this exercise is meant to give some insight into what kinds of numbers can be the hypotenuse of a primitive pythagorean triple. A pythagorean triple is called primitive if its three members have no common divisors, so that they are relatively prime. some triples listed above are primitive. A primitive pythagorean triple is a pythagorean triple (a,b,c) such that gcd (a,b,c)=1, where gcd is the greatest common divisor. a right triangle whose side lengths give a primitive pythagorean triple is then known as a primitive right triangle. Question: if (a,b,c) is a primitive pythagorean triple, the number c is called the hy potenuse of the triple, for reasons that should be self explanatory. this ex ercise is meant to give some insight into what kinds of numbers can be the hypotenuse of a primitive pythagorean triple.
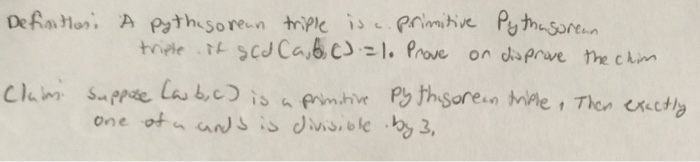
Solved Definition A Pythagorean Triple Is A Primitive Chegg If (a,b,c) is a primitive pythagorean triple, the number c is called the hypotenuse of the triple, for reasons that should be self explanatory. this exercise is meant to give some insight into what kinds of numbers can be the hypotenuse of a primitive pythagorean triple. A pythagorean triple is called primitive if its three members have no common divisors, so that they are relatively prime. some triples listed above are primitive. A primitive pythagorean triple is a pythagorean triple (a,b,c) such that gcd (a,b,c)=1, where gcd is the greatest common divisor. a right triangle whose side lengths give a primitive pythagorean triple is then known as a primitive right triangle. Question: if (a,b,c) is a primitive pythagorean triple, the number c is called the hy potenuse of the triple, for reasons that should be self explanatory. this ex ercise is meant to give some insight into what kinds of numbers can be the hypotenuse of a primitive pythagorean triple.

Solved A Pythagorean Triple Is A Triple A B C Of Positive Chegg A primitive pythagorean triple is a pythagorean triple (a,b,c) such that gcd (a,b,c)=1, where gcd is the greatest common divisor. a right triangle whose side lengths give a primitive pythagorean triple is then known as a primitive right triangle. Question: if (a,b,c) is a primitive pythagorean triple, the number c is called the hy potenuse of the triple, for reasons that should be self explanatory. this ex ercise is meant to give some insight into what kinds of numbers can be the hypotenuse of a primitive pythagorean triple.
Comments are closed.