Solved Given 2 Vectors P Q And Given That The Magnitude Chegg

Solved Given 2 Vectors P Q And Given That The Magnitude Chegg Given 2 vectors p & q of equal magnitude, pointing at 45° and 45° from vertical respectively, determine the vertical component of the resultant vector calculated by subtracting q from p. How do you find the resultant magnitude of two vectors? the magnitude of the resultant vector can be found by using the law of cosines. the formula is: r = √ (a^2 b^2 2abcosθ), where a and b are the magnitudes of the original vectors,and θ is the angle between the vectors.

Given The Vectors P And Q Shown On The Grid Chegg Given two vectors p and q of equal magnitude, and the relationship ∣p q∣ = n∣p −q∣. we need to find the angle θ between them. let the magnitude of both vectors be p. so, ∣p ∣ = ∣q∣ = p. let the angle between them be θ. find ∣p q∣ using the cosine law for vectors: ∣p q∣ = p 2 q2 2pqcosθ = 2p 2 2p 2cosθ. since p = q,. Step 4: find the magnitude of the resultant vector now, we need to find the magnitude of the resultant vector when →p is added to a vector →b that is perpendicular to →p and equal in magnitude to →q. Given 2 vectors p & q, and given that the magnitude of q is 2 times the magnitude of p, determine the magnitude of the resultant vector of adding p & q if they are aligned in the same direction. Our expert help has broken down your problem into an easy to learn solution you can count on. there are 3 steps to solve this one. the problem covers two vectors in a two dimensional environment. we ha not the question you’re looking for? post any question and get expert help quickly.
Solved Given The Two Vectors Of The Following Figure What Chegg Given 2 vectors p & q, and given that the magnitude of q is 2 times the magnitude of p, determine the magnitude of the resultant vector of adding p & q if they are aligned in the same direction. Our expert help has broken down your problem into an easy to learn solution you can count on. there are 3 steps to solve this one. the problem covers two vectors in a two dimensional environment. we ha not the question you’re looking for? post any question and get expert help quickly. Therefore, to solve this question, we shall use the triangle rule for vector to calculate the angle between vectors p and q. formula used: c 2 = a 2 b 2 where, c is the hypotenuse a and b are opposite and adjacent sides. complete step by step solution: it is given that the magnitude of resultant vector p makes an angle of tan 1 (3 4). 2.7 rectangular components of vectors; unit vectors • for ease in mathematical manipulation, forces (and vectors) can be resolved into rectangular components along predefined x, y (and z) directions. We have two vectors, →p and →q. the resultant of these two vectors is equal to the magnitude of →q. this can be expressed mathematically as: where α is the angle between →p and →q. now, we double the magnitude of →q. let the new vector be →q′ = 2q. we need to find the new resultant r′ and the angle θ made by r′ with →p. In our case, we're given three vectors, p →, q →, and r →, that add up to zero: p → q → r → = 0. this scenario implies that these vectors form a closed triangle when placed tip to tail.
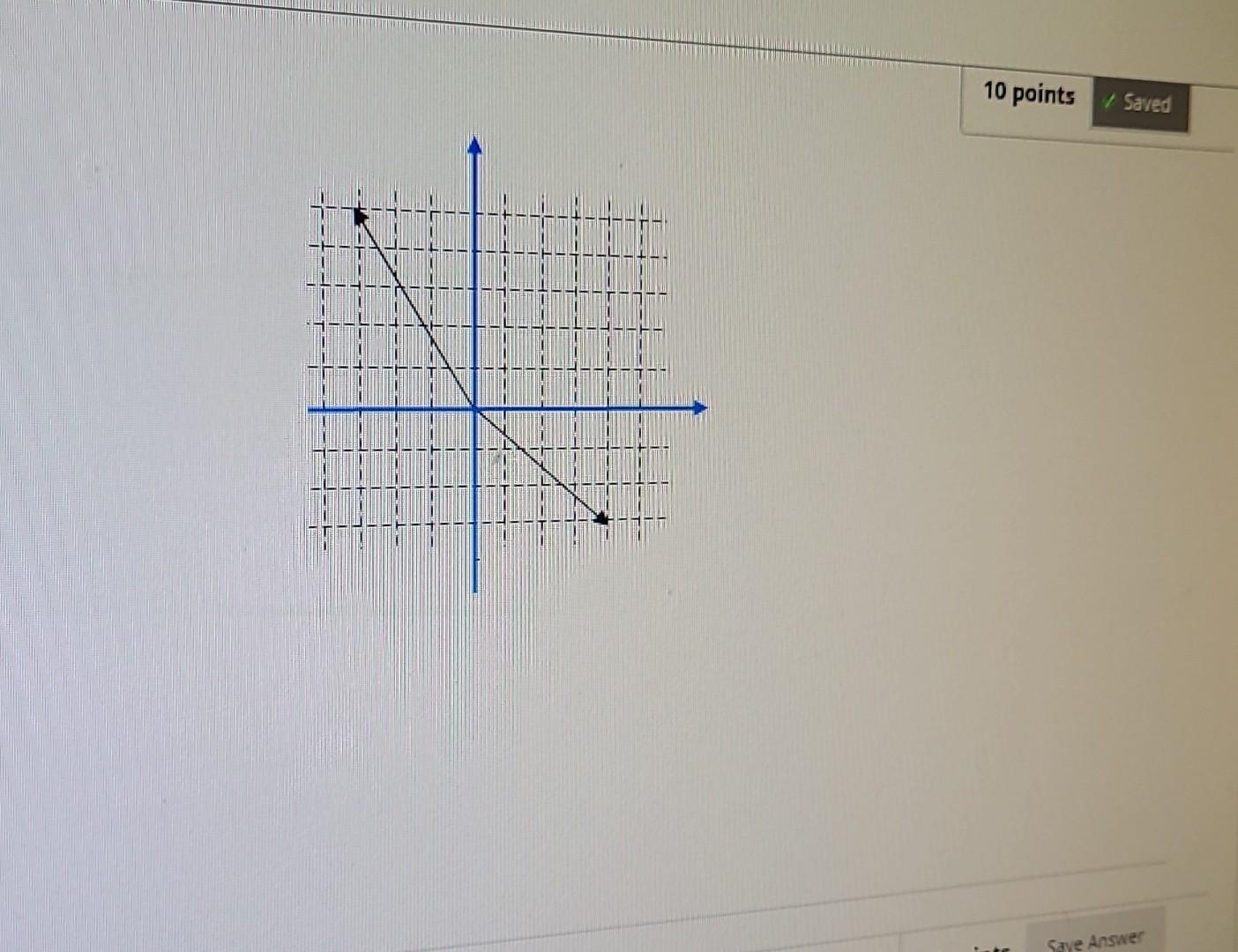
Solved Given The Two Vectors Of The Following Figure What Chegg Therefore, to solve this question, we shall use the triangle rule for vector to calculate the angle between vectors p and q. formula used: c 2 = a 2 b 2 where, c is the hypotenuse a and b are opposite and adjacent sides. complete step by step solution: it is given that the magnitude of resultant vector p makes an angle of tan 1 (3 4). 2.7 rectangular components of vectors; unit vectors • for ease in mathematical manipulation, forces (and vectors) can be resolved into rectangular components along predefined x, y (and z) directions. We have two vectors, →p and →q. the resultant of these two vectors is equal to the magnitude of →q. this can be expressed mathematically as: where α is the angle between →p and →q. now, we double the magnitude of →q. let the new vector be →q′ = 2q. we need to find the new resultant r′ and the angle θ made by r′ with →p. In our case, we're given three vectors, p →, q →, and r →, that add up to zero: p → q → r → = 0. this scenario implies that these vectors form a closed triangle when placed tip to tail.
Comments are closed.