Solved For The Unit Step Response Of A Second Order System Chegg

Solved 2 The Unit Step Response Of A Second Order System Is Chegg The goal is to evaluate the unit step response of the second order control system shown in fig. q2, i.e., when r(s)= s1. q2 (a) match the transfer function of the system to the standard form of a second order system and find natural frequency (ωn) and damping ratio (ζ) of the system. Below is a plot of the unit step response for a second order system with ω n = 1 and different values of ζ: the unit step response of a second order system provides insight into the system's behavior, such as its stability, speed of response, and oscillation characteristics.
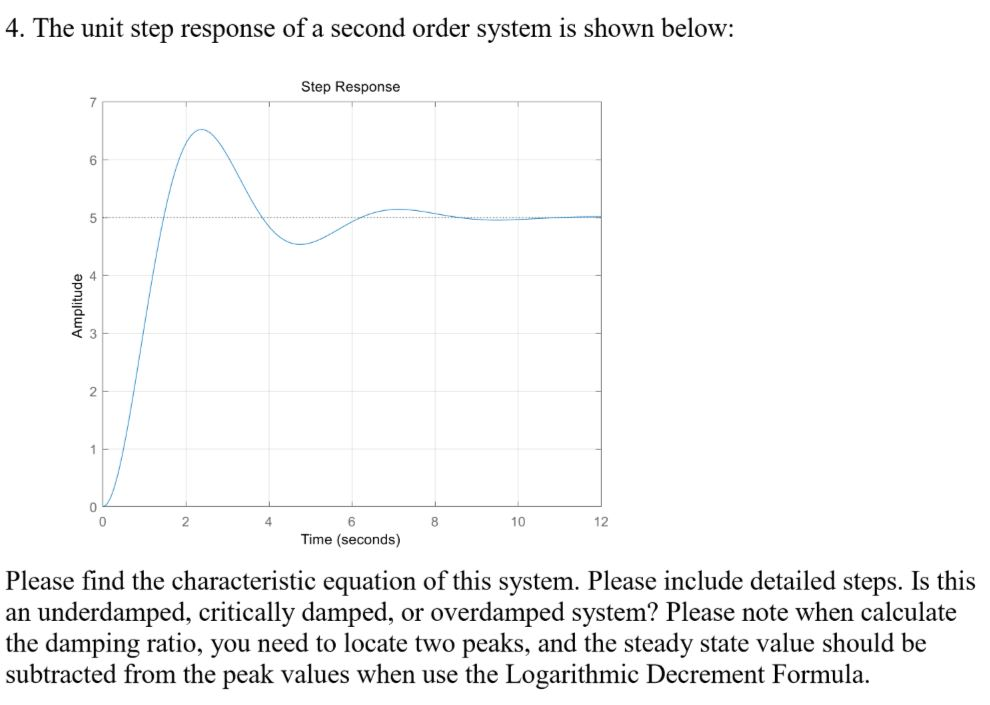
Solved 4 The Unit Step Response Of A Second Order System Is Chegg Follow these steps to get the response (output) of the second order system in the time domain. take laplace transform of the input signal, $r (t)$. substitute $r (s)$ value in the above equation. do partial fractions of $c (s)$ if required. apply inverse laplace transform to $c (s)$. Equation (5) represents the response of the system for a given step input. the matlab sequence to obtain the step response for a given ‘l’, ‘k’ and ‘b’ is given below. For the unit step response of second order system following statements are given: (a) delay time is the time required for the response to reach 60% of the final value in first attempt. The claim that we get a continuous response is true, but may feel a bit unjustified. let’s redo the above example very carefully without making this assumption.
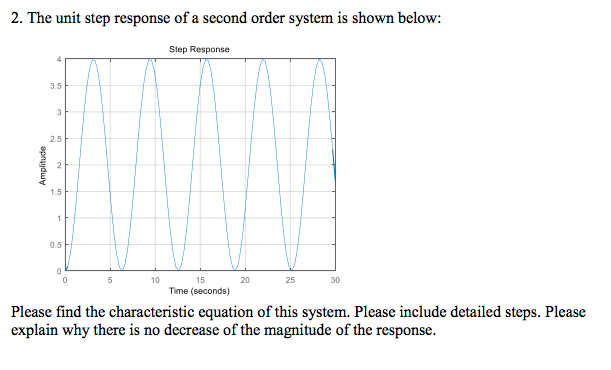
Solved 2 The Unit Step Response Of A Second Order System Is Chegg For the unit step response of second order system following statements are given: (a) delay time is the time required for the response to reach 60% of the final value in first attempt. The claim that we get a continuous response is true, but may feel a bit unjustified. let’s redo the above example very carefully without making this assumption. The term 95% response time sometimes is used to refer to this case. also, values of ±1% sometimes are used. overshoot: os = a b (% overshoot is 100a b). decay ratio: dr = c a (where c is the height of the second peak). period of oscillation: p is the time between two successive peaks or two successive valleys of the response. Using this as a base, we will analyze the time response of a second order control system. we’ll do this by analyzing the unit step response of a second order control system in the frequency domain, before converting it into the time domain. In this case, ζ = 0.591 and ωn = 1.13 rad s. the transfer function of a second order system can be written as g (s) = k (s^2 2ζωn s ωn^2), where k is the static gain. therefore, the transfer function is g (s) = 3.5 (s^2 2 * 0.591 * 1.13 s 1.13^2). Let us consider a second order control system in which a unit step input signal is given and it is also considered that the system is initially at rest. that is all initial conditions of the system are zero. the time response characteristics of the system at underdamped condition is drawn below.
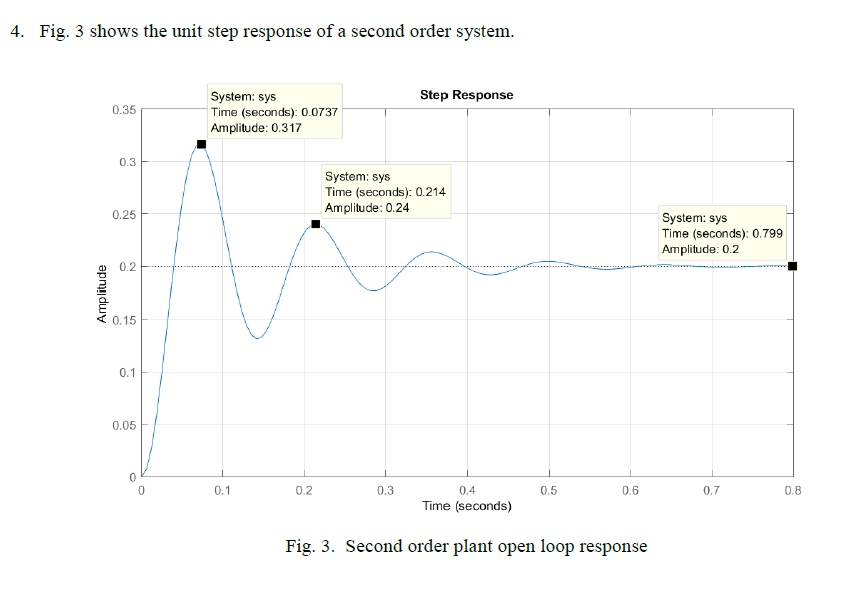
Solved 4 Fig 3 Shows The Unit Step Response Of A Second Chegg The term 95% response time sometimes is used to refer to this case. also, values of ±1% sometimes are used. overshoot: os = a b (% overshoot is 100a b). decay ratio: dr = c a (where c is the height of the second peak). period of oscillation: p is the time between two successive peaks or two successive valleys of the response. Using this as a base, we will analyze the time response of a second order control system. we’ll do this by analyzing the unit step response of a second order control system in the frequency domain, before converting it into the time domain. In this case, ζ = 0.591 and ωn = 1.13 rad s. the transfer function of a second order system can be written as g (s) = k (s^2 2ζωn s ωn^2), where k is the static gain. therefore, the transfer function is g (s) = 3.5 (s^2 2 * 0.591 * 1.13 s 1.13^2). Let us consider a second order control system in which a unit step input signal is given and it is also considered that the system is initially at rest. that is all initial conditions of the system are zero. the time response characteristics of the system at underdamped condition is drawn below.
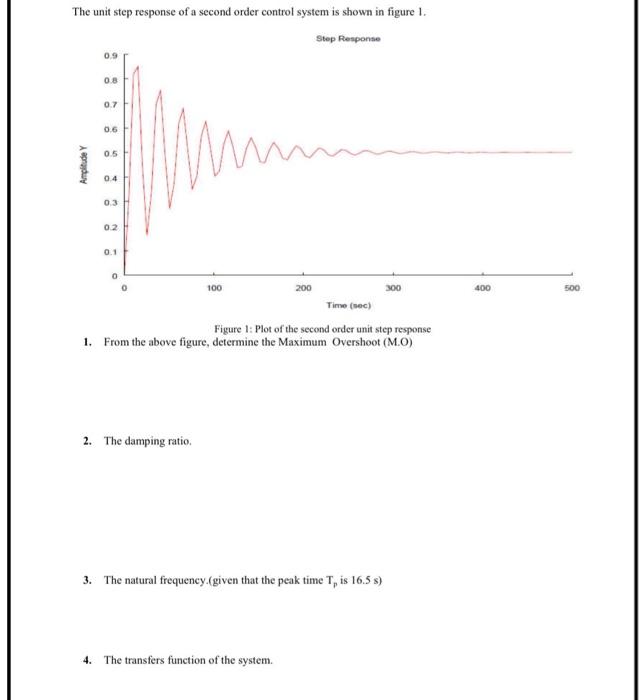
Solved The Unit Step Response Of A Second Order Control Chegg In this case, ζ = 0.591 and ωn = 1.13 rad s. the transfer function of a second order system can be written as g (s) = k (s^2 2ζωn s ωn^2), where k is the static gain. therefore, the transfer function is g (s) = 3.5 (s^2 2 * 0.591 * 1.13 s 1.13^2). Let us consider a second order control system in which a unit step input signal is given and it is also considered that the system is initially at rest. that is all initial conditions of the system are zero. the time response characteristics of the system at underdamped condition is drawn below.
Comments are closed.