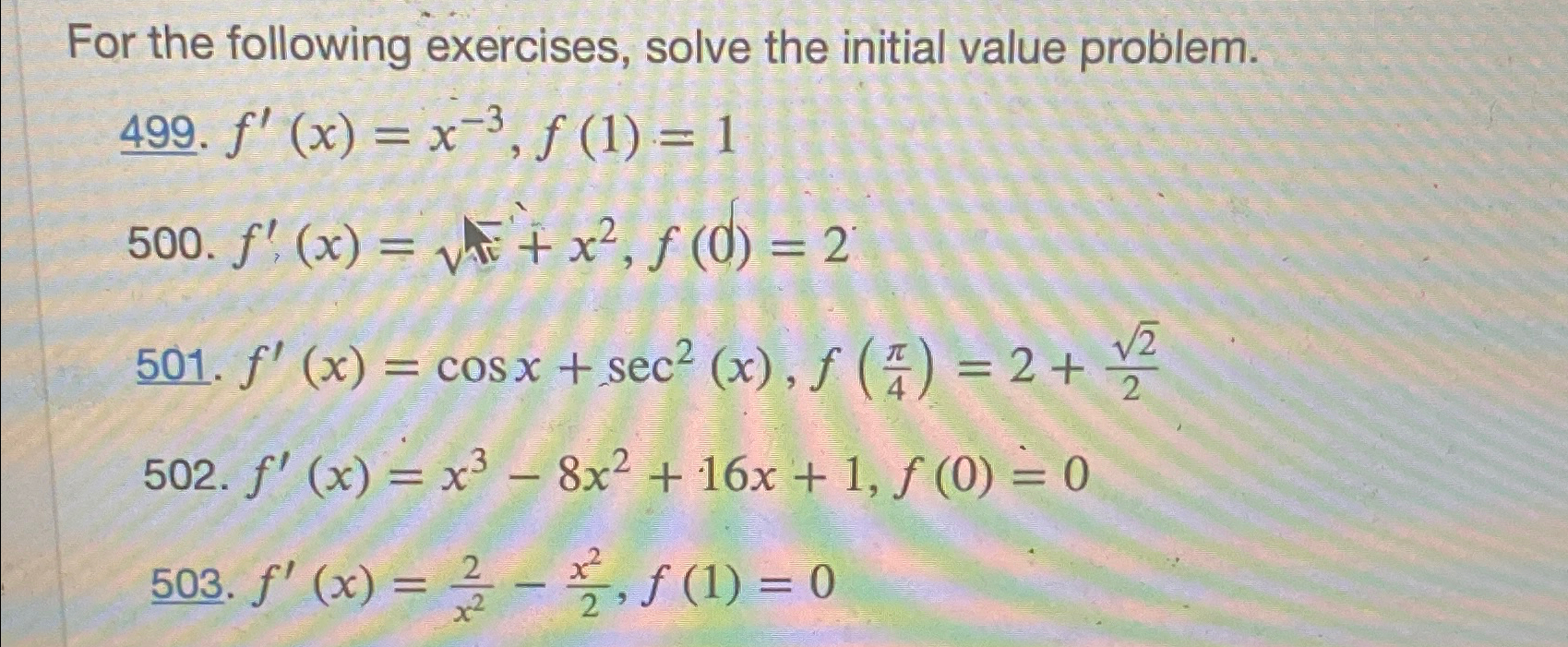
Solved For The Following Exercises Solve The Initial Value Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. there are 2 steps to solve this one. given that , f ′ (x) = x 3 , f (1) = 1 . not the question you’re looking for? post any question and get expert help quickly. This page titled 8.3e: solution of initial value problems (exercises) is shared under a cc by nc sa 3.0 license and was authored, remixed, and or curated by william f. trench.
Solved For The Following Exercises Solve The Initial Value Chegg Activity 6.2.1. solving linear differential equations with laplace transforms. use laplace transforms to solve each of the following initial value problems. Solution: in this example the forcing function has the graph shown in figure 6.4.2 and is known as ramp loading. is is relatively easy to identify the general form of the solution. for t <5 t <5, the solution is simply y = 0 y = 0. on the other hand, for t> 10 t> 10, the solution has the form. The goal of this section is to use laplace transform to solve initial value problems, in second order linear ode (as in chapter 3). this way, the methods may become more algebraic. two theorem that follows would be instrumental for this method. This calculus video tutorial explains how to solve the initial value problem as it relates to separable differential equations. more.
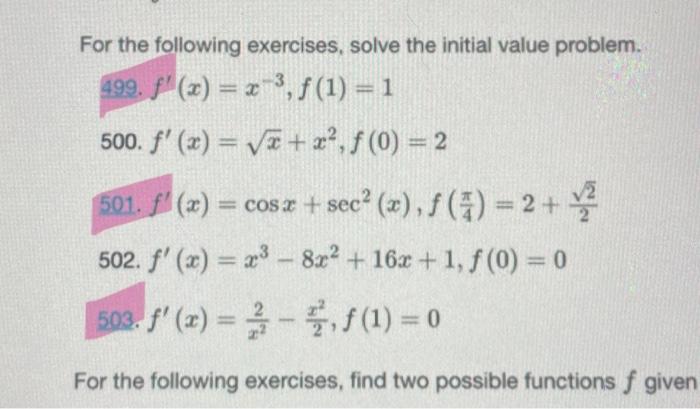
Solved For The Following Exercises Solve The Initial Value Chegg The goal of this section is to use laplace transform to solve initial value problems, in second order linear ode (as in chapter 3). this way, the methods may become more algebraic. two theorem that follows would be instrumental for this method. This calculus video tutorial explains how to solve the initial value problem as it relates to separable differential equations. more. There are 3 steps to solve this one. consider the following initial value problem. finding the laplace transform of the solution of the gi not the question you’re looking for? post any question and get expert help quickly. We look at techniques for integrating a large variety of functions involving products, quotients, and compositions later in the text. here we turn to one common use for antiderivatives that arises often in many applications: solving differential equations. This section applies the laplace transform to solve initial value problems for constant coefficient second order differential equations on (0,∞). Solving initial value problems with laplace transforms we will solve differential equations with constant coefficients using laplace transforms by transforming the differential equation.
Comments are closed.