Solved Find The Minimum Sample Size You Should Use To Assure Chegg

Solved Find The Minimum Sample Size You Should Use To Assure Chegg Use the margin of error, confidence level, and standard deviation s to find the minimum sample size required to estimate an unknown population mean . margin of error: $139, confidence level: 95%, s = $513. To find the minimum sample size required to estimate a population proportion (p), we can use the formula based on the margin of error (moe), the critical value for the specified confidence level, and the estimated proportion from prior studies.

Solved Find The Minimum Sample Size You Should Use To Assure Chegg Find the minimum sample size you should use to assure that your estimate of p will be within the required margin of error around the population p. Answer on question #48383 math statistics and probability answer on question #48383 – math statistics and probability find the minimum sample size you should. Minimum sample size required calculator – estimating the population mean instructions: this calculator finds the minimum sample size required to estimate the population mean (μ μ) within a specified margin of error. Our expert help has broken down your problem into an easy to learn solution you can count on. question: find the minimum sample size you should use to assure that your estimate of p will be within the required margin of error around the population p. a margin of error: 0.044; confidence level: 95%; 22 and 9 are unknown 12 496 497.
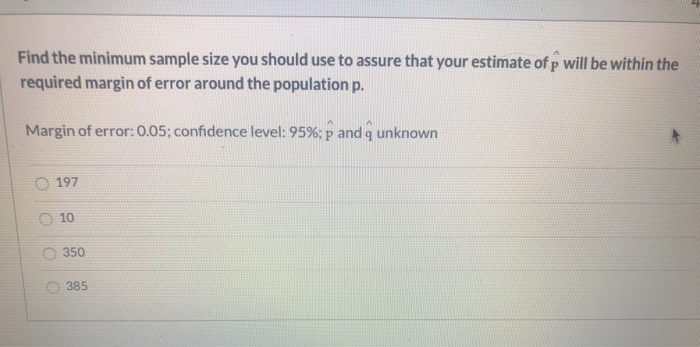
Solved Find The Minimum Sample Size You Should Use To Assure Chegg Minimum sample size required calculator – estimating the population mean instructions: this calculator finds the minimum sample size required to estimate the population mean (μ μ) within a specified margin of error. Our expert help has broken down your problem into an easy to learn solution you can count on. question: find the minimum sample size you should use to assure that your estimate of p will be within the required margin of error around the population p. a margin of error: 0.044; confidence level: 95%; 22 and 9 are unknown 12 496 497. To construct the confidence interval, we can use the formula p ± z*sqrt (p*q n), where p is the sample proportion (478 976 = 0.489), q is 1 p, n is the sample size (976), and z is the z score for the given confidence level (in this case, 1.96 for 95%). [solved] find the minimum sample size you should use to assure that your estimate of p will be within the required margin of error around the population. Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. see answer. Find the minimum sample size you should use to assure that your estimate will be within the required margin of error around the population mean. margin of error: 0.002; confidence level: 93%; p and q unknown.

Solved Find The Minimum Sample Size You Should Use To Assure Chegg To construct the confidence interval, we can use the formula p ± z*sqrt (p*q n), where p is the sample proportion (478 976 = 0.489), q is 1 p, n is the sample size (976), and z is the z score for the given confidence level (in this case, 1.96 for 95%). [solved] find the minimum sample size you should use to assure that your estimate of p will be within the required margin of error around the population. Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. see answer. Find the minimum sample size you should use to assure that your estimate will be within the required margin of error around the population mean. margin of error: 0.002; confidence level: 93%; p and q unknown.

Solved Find The Minimum Sample Size You Should Use To Assure Chegg Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. see answer. Find the minimum sample size you should use to assure that your estimate will be within the required margin of error around the population mean. margin of error: 0.002; confidence level: 93%; p and q unknown.
Comments are closed.