Solved Find The Gcd For The Given Numbers By An Appropriate Chegg

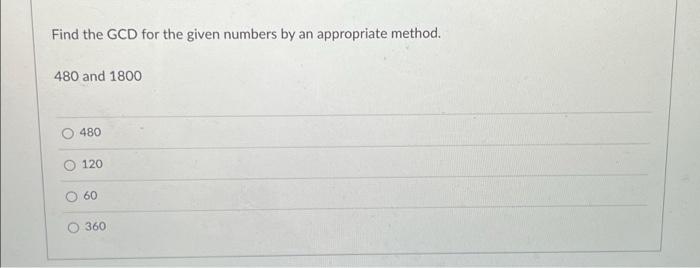
Solved Find The Gcd For The Given Numbers By An Appropriate Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. here’s the best way to solve it. not the question you’re looking for? post any question and get expert help quickly. To find the **gcd (greatest common divisor) **between two numbers, such as 480 and 180, we can use the euclidean algorithm. the euclidean algorithm involves repeatedly dividing the larger number by the smaller number and taking the remainder until the remainder is zero.

Solved Find The Gcd For The Given Numbers By An Appropriate Chegg Step 1: identify the appropriate method to find the gcd (greatest common divisor) the question asks to find the gcd for the given numbers 84 and 378. the appropriate method to find the gcd of two numbers is the euclidean algorithm. Solution answer: the greatest common divisor (gcd) for the given numbers 240, 5000, and 4500 is 2000. step 1: find the prime factorization of each number. 240 = 2^4 * 3 * 5 5000 = 2^3 * 5^4 4500 = 2^2 * 3^2 * 5^3 step 2: identify the common prime factors and their smallest exponent. the common prime factors are 2, 3, and 5. Use this page to calculate the gcd of a set of two or more numbers. The gcd calculator uses 4 methods to find the greatest common divisor of two or more integers.

Solved Find The Gcd For The Given Numbers By An Appropriate Chegg Use this page to calculate the gcd of a set of two or more numbers. The gcd calculator uses 4 methods to find the greatest common divisor of two or more integers. I have to find the greatest common divisor of $a=78$ and $b=132$. i have worked out to $$\begin {align} 132 & = 78 \times 1 54 \\ 78 & = 54 \times 1 24 \\ 54 & = 24 \times 2 6. I know that gcd (a,a) = a itself but the problem here is, that the individual gcd given are in a random order, and therefore, i don't know which input number is the gcd of which two numbers. This calculator computes the greatest common divisor factor (gcd or gcf) of two or more integers. it also shows the solution process of two methods. This easy to use greatest common divisor (gcd) and least common multiple (lcm) calculator easily computes the gcd and lcm for any given set of numbers and generates an in depth solution for the purposes of analysis.