Solved Example 1 Instantaneous Velocity And Tangent Lines A Chegg

Solved Example 1 Instantaneous Velocity And Tangent Lines A Chegg Example 1 instantaneous velocity and tangent lines a rock is launched vertically upward from the ground with an initial speed of 96ft s. the position of the rock in feet above the ground after t seconds is given by the function s(t)=−16t2 96t. Instantaneous velocity is the limit of average velocity as the length of the time interval shrinks to zero. graphically, instantaneous velocity at time t is the slope of the tangent line to the graph of position as a function of time.
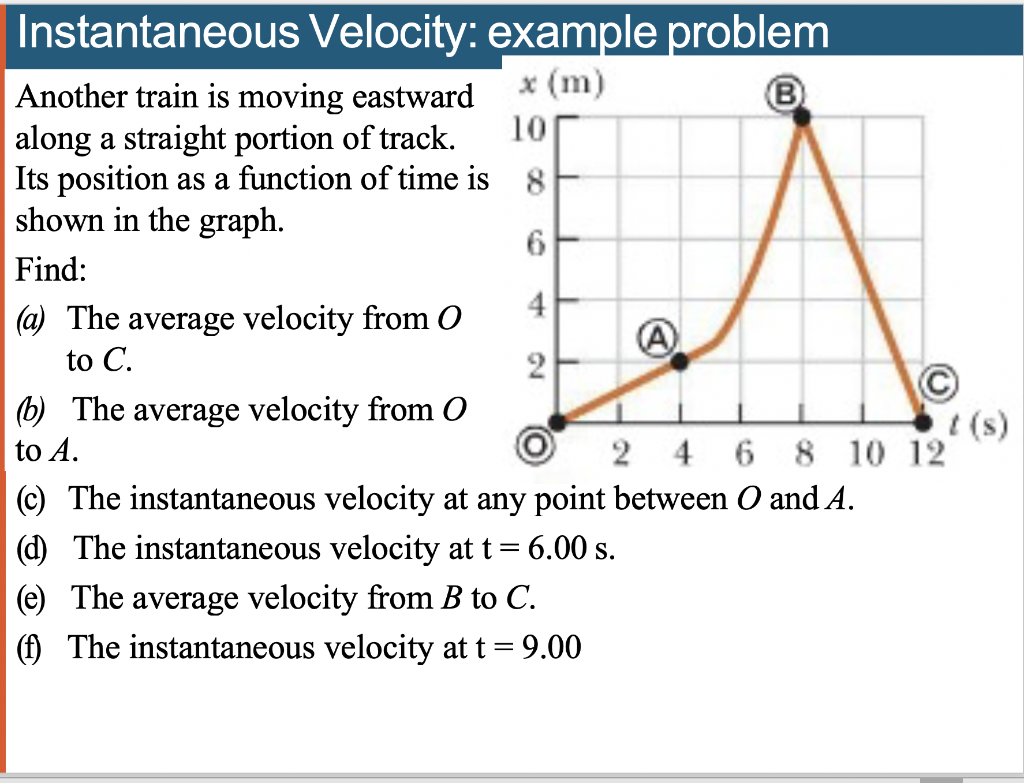
Solved How To Draw Tangent Line Step By Step To Solve The Chegg Example if a ball is thrown into the air with a velocity of 40 ft s, its height in feet after t seconds is given by y = 40t−16t2. Y over smaller and smaller time intervals. given a graph of a position function, the slope of the secant line gives us average velocity and the slope of the tan. We explain practice calculating instantaneous velocity with video tutorials and quizzes, this lesson provides the learner with example problems on calculating the instantaneous speed and velocity of an object. For example, before you can compute the instantaneous velocity you need to know the average velocity in terms of an unknown quantity. look for given values of your independent variable (usually x or t in these problems) and compute their other component via the given expression.

Solved Lesson03 2 1 Instant Velocity Tangent Lines 1 Point Chegg We explain practice calculating instantaneous velocity with video tutorials and quizzes, this lesson provides the learner with example problems on calculating the instantaneous speed and velocity of an object. For example, before you can compute the instantaneous velocity you need to know the average velocity in terms of an unknown quantity. look for given values of your independent variable (usually x or t in these problems) and compute their other component via the given expression. Example suppose a ball is dropped from a height of 200 feet. if tis the time after the ball was released, measured in seconds, and sis the height of the ball above the ground at time t, then s= 200 16t2: suppose we want to know the (instantaneous) velocity vof the ball at time t= 2. Question: 1. instantaneous velocity can also be found graphically from the slope of the tangent line drawn to the x versus tcurve. draw a tangent to your curve (graph 1 ), at two different instants of time. calculate slope of the tangent line showing your calculations on the graph. Height versus time. the instantaneous velocity at a particular time and height is the slope of the tangent line to the graph at the point given by that time and height. This page covers instantaneous and average velocity using examples from races and swimming. it defines instantaneous velocity as speed at a specific moment, noting that in constant velocity motion, ….

Solved Lesson03 2 1 Instant Velocity Tangent Lines 1 Point Chegg Example suppose a ball is dropped from a height of 200 feet. if tis the time after the ball was released, measured in seconds, and sis the height of the ball above the ground at time t, then s= 200 16t2: suppose we want to know the (instantaneous) velocity vof the ball at time t= 2. Question: 1. instantaneous velocity can also be found graphically from the slope of the tangent line drawn to the x versus tcurve. draw a tangent to your curve (graph 1 ), at two different instants of time. calculate slope of the tangent line showing your calculations on the graph. Height versus time. the instantaneous velocity at a particular time and height is the slope of the tangent line to the graph at the point given by that time and height. This page covers instantaneous and average velocity using examples from races and swimming. it defines instantaneous velocity as speed at a specific moment, noting that in constant velocity motion, ….
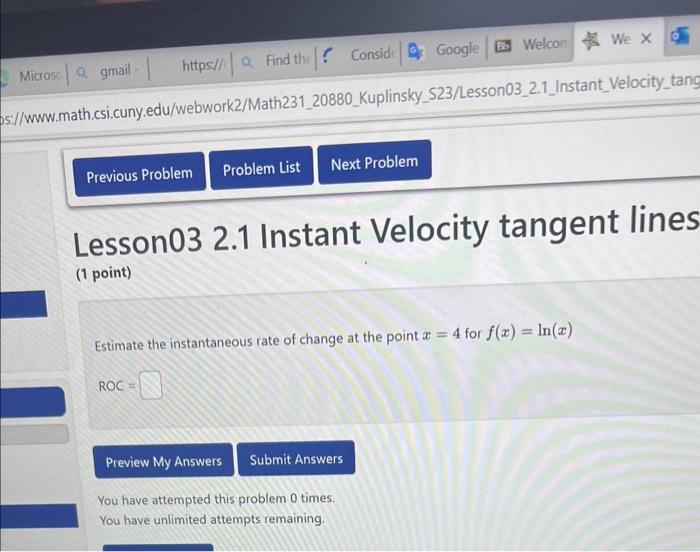
Solved Lesson03 2 1 Instant Velocity Tangent Lines 1 Point Chegg Height versus time. the instantaneous velocity at a particular time and height is the slope of the tangent line to the graph at the point given by that time and height. This page covers instantaneous and average velocity using examples from races and swimming. it defines instantaneous velocity as speed at a specific moment, noting that in constant velocity motion, ….
Comments are closed.