Solved Diagonalize The Following Matrix If Possible 6 0 10 Chegg

Solved Diagonalize The Following Matrix If Possible 6 0 Chegg Question: diagonalize the following matrix, if possible. 6 0 10 6 6 0 oa for p= d= 05 60 6 0 b. for p= 1 d= 5 1 0 6 10 0 o c. for p= ,d= 0 10 d. the matrix cannot be diagonalized. On this post you will find everything about diagonalizable matrices: what diagonalizable matrices are, when a matrix can and cannot be diagonalized, how to to diagonalize matrices,… and you even have several problems solved step by step so that you can practice and understand perfectly how to do it.

Solved Diagonalize The Following Matrix If Possible 6 0 10 Chegg We explain how to diagonalize a matrix if possible. step by step procedure of the diagonalization together with an example is given. new problems are added. The matrix a is diagonalizable if and only if the sum of the dimensions of the distinct eigenspaces equals n, and this happens if and only if the dimension of the eigenspace for each k equals the multiplicity of k. As we only have 2 distinct eigenvalues, we need more information to determine if the matrix is diagonalizable. i was using the following condition to determine this: a linear transformation, $a$, is diagonalizable if and only if $v$ has a basis of eigenvectors of $a$. Answered step by step solved by verified expert western university • math • math 1600.

Solved Diagonalize The Following Matrix If Possible 6 0 Chegg As we only have 2 distinct eigenvalues, we need more information to determine if the matrix is diagonalizable. i was using the following condition to determine this: a linear transformation, $a$, is diagonalizable if and only if $v$ has a basis of eigenvectors of $a$. Answered step by step solved by verified expert western university • math • math 1600. Matrix diagonalization is the process of reducing a square matrix into its diagonal form using a similarity transformation. this process is useful because diagonal matrices are easier to work with, especially when raising them to integer powers. not all matrices are diagonalizable. Figure 4.3.1. the matrix \ (a\) has the same geometric effect as the diagonal matrix \ (d\) when expressed in the coordinate system defined by the basis of eigenvectors. now that we have developed some algebraic techniques for finding eigenvalues and eigenvectors, we will explore this observation more deeply. in particular, we will make precise the sense in which \ (a\) and \ (d\) are. Compute the characteristic polynomial p ( ) = det(a i). its roots are the eigenvalues of a. if p ( ) does not have n real roots, counting multiplicities (in other words, if it has some complex roots), then a is not diagonalizable. Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with step by step explanations, just like a math tutor.

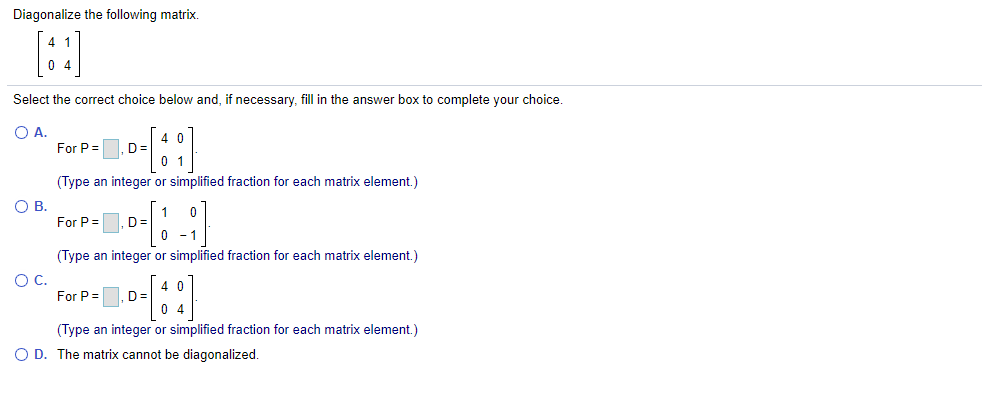
Solved Diagonalize The Following Matrix If Possible 6 0 10 Chegg Matrix diagonalization is the process of reducing a square matrix into its diagonal form using a similarity transformation. this process is useful because diagonal matrices are easier to work with, especially when raising them to integer powers. not all matrices are diagonalizable. Figure 4.3.1. the matrix \ (a\) has the same geometric effect as the diagonal matrix \ (d\) when expressed in the coordinate system defined by the basis of eigenvectors. now that we have developed some algebraic techniques for finding eigenvalues and eigenvectors, we will explore this observation more deeply. in particular, we will make precise the sense in which \ (a\) and \ (d\) are. Compute the characteristic polynomial p ( ) = det(a i). its roots are the eigenvalues of a. if p ( ) does not have n real roots, counting multiplicities (in other words, if it has some complex roots), then a is not diagonalizable. Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with step by step explanations, just like a math tutor.