Solved Construct The Following Using A Compass And A Chegg Construct the following using a compass and a straightedge. 1. a triangle with side equal to these three segments. 2. a square with one of its sides is 3. a regular pentagon with side equal to 3 cm 4. a regular hexagon with side equal to 0.5 inch. Suppose we wish to construct a perpendicular bisector of the line segment ef. we can correctly begin by placing the compass on point e and marking off the distance to which point?.
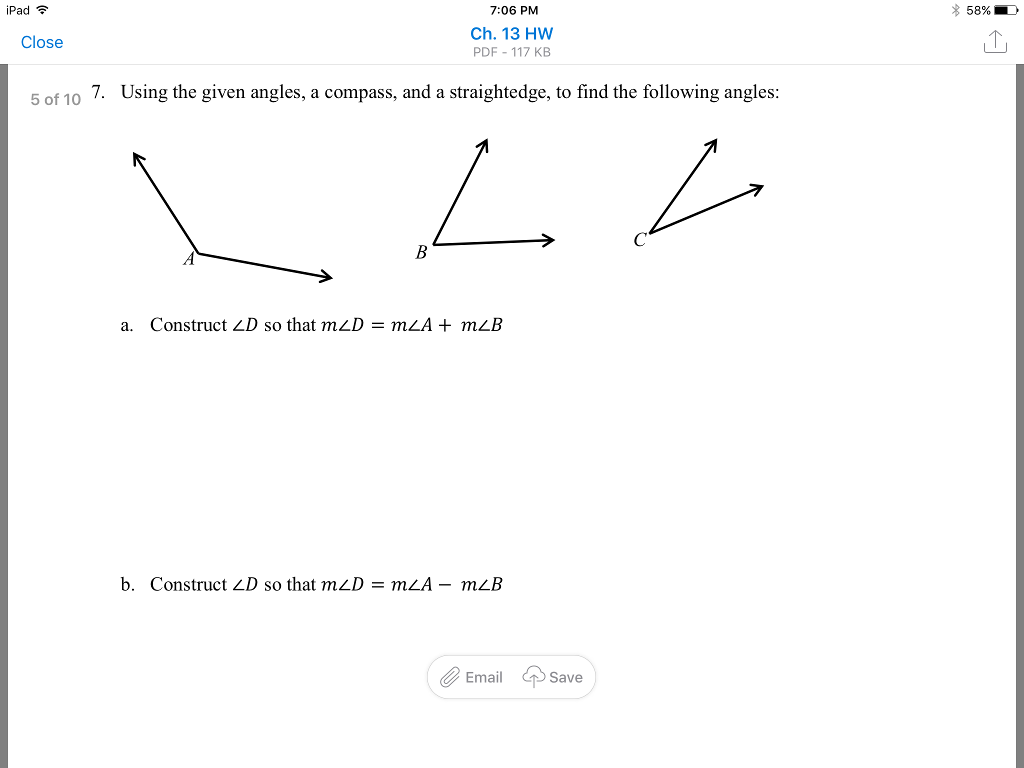
Solved Using The Given Angles A Compass And A Chegg To construct angle bisector, pin the compass to point a, then create small arc to line segment ad and line segment ab. the intersection of the line segment and the small arc will create points. Question answered step by step refer to the figure shown and, using only a compass and a straightedge, perform each of the following constructions. a. construct $\angle c$ so that $m (\angle c)=2 m (\angle a) m (\angle b)$. b. construct $\angle c$ so that $m (\angle c)=2 m (\angle b) m (\angle a)$. instant solution:. Now you can see why the greeks couldn't determine that trisecting an angle with straightedge and compass is impossible. our solution requires a lot of algebra that was just not available 2000 years ago. The constructions only permit to use a ruler and a compass. my question arises due to a statement in the book hardy and wright, which is as follows : euclidean constructions by ruler and compass are equivalent analytically to solutions of a series of linear or quadratic equations.
Solved 7 Refer To The Figure Shown And Using Only A Chegg Now you can see why the greeks couldn't determine that trisecting an angle with straightedge and compass is impossible. our solution requires a lot of algebra that was just not available 2000 years ago. The constructions only permit to use a ruler and a compass. my question arises due to a statement in the book hardy and wright, which is as follows : euclidean constructions by ruler and compass are equivalent analytically to solutions of a series of linear or quadratic equations. Based on the information provided, mason wants to construct a segment fg that is congruent to segment be. in geometry, congruent means having the same size and shape. Study with quizlet and memorize flashcards containing terms like type 1: perpendicular bisector of a segment, type 2: perpendicular through a point on the line, type 3: perpendicular through a point not on the line and more. 1. a 255 degree angle (documenting all steps) 2. an equilateral triangle and its 90 degree, clockwise rotation around a center of rotation of your choice (where the center of rotation is not on the original figure, and is marked in a different color) there are 2 steps to solve this one. The student will use a compass and straightedge to demonstrate that the perpendicular bisectors of the three angles of a triangle intersect at a point which is the center of the circle that inscribes the triangle.
Comments are closed.