Solved Consider The One Link Robot In Figure 1 The Jacobian Chegg

Solved Consider The One Link Robot In Figure 1 The Jacobian Chegg Consider the one link robot in figure 1. the jacobian linearization of the robot about the equilibrium point z∗ =[2π 0] and u∗ =0 was derived in pset1 as: a= [0 img 1 −ib], b =[0 i1] figure 1: single link robot a) assume m=0.1,i =1,b=2, and g= 10, and all the states are individually measured. Problem 1 (30 points). consider the puma robot depicted in figure 1, where the dh coordinate frames have already been defined. derive the jacobian matrix for this robot which relates joint velocities to end effector velocities.

Solved Consider The Same Single Link Robot In Figure 1 With Chegg Consider the three link cylindrical robot represented symbolically by the following figure. Since the elements of the jacobian matrix are functions of joint displacements, the inverse jacobian varies depending on the arm configuration. this means that although the desired end effecter velocity is constant, the joint velocities are not. Robot 1: m, robot 2: m, robot a = robot b = 0.4 m. the left two link planar robot is attempting to transfer a small object labeled p to the similar right robot. The jacobian linearization of the robot about the equilibrium point z* and u* = 0 was derived in pset1 as: ma figure 1: single link robot a) assume m = 0.1, i = 1, b = 2, and q = 10, and all the states are individually measured.

Solved Consider The One Link Robot In Figure 2 Where θ Chegg Robot 1: m, robot 2: m, robot a = robot b = 0.4 m. the left two link planar robot is attempting to transfer a small object labeled p to the similar right robot. The jacobian linearization of the robot about the equilibrium point z* and u* = 0 was derived in pset1 as: ma figure 1: single link robot a) assume m = 0.1, i = 1, b = 2, and q = 10, and all the states are individually measured. As a constant, the above is just a linear system of four equations and four unknowns (the ai’s), and it can be solved with a little simple algebra to yield: a0 = θ0 a1 = 0. Consider the one link robot in figure 1. the jacobian linearization of the robot about the equilibrium point z∗= [2π0] and u∗=0 was derived in pset1 as: a= [0img1−ib],b= [0i1] figure 1: single link robot a) assume m=0.1,i=1,b=2, and g=10, and all the states are individually measured. Time to understand the jacobian matrix. columns of the jacobian matrix are associated with joints of the robot. each column in the jacobian matrix represents the effect on end effector velocities due to variation in each joint velocity. Hint: you should model these euler angles as the product of three revolute joints along the x; y; z axes and show that when the second angle is =2 the jacobian loses rank.

Solved 3 Consider The Two Link Robot In Figure 2 Fig 2 A Chegg As a constant, the above is just a linear system of four equations and four unknowns (the ai’s), and it can be solved with a little simple algebra to yield: a0 = θ0 a1 = 0. Consider the one link robot in figure 1. the jacobian linearization of the robot about the equilibrium point z∗= [2π0] and u∗=0 was derived in pset1 as: a= [0img1−ib],b= [0i1] figure 1: single link robot a) assume m=0.1,i=1,b=2, and g=10, and all the states are individually measured. Time to understand the jacobian matrix. columns of the jacobian matrix are associated with joints of the robot. each column in the jacobian matrix represents the effect on end effector velocities due to variation in each joint velocity. Hint: you should model these euler angles as the product of three revolute joints along the x; y; z axes and show that when the second angle is =2 the jacobian loses rank.

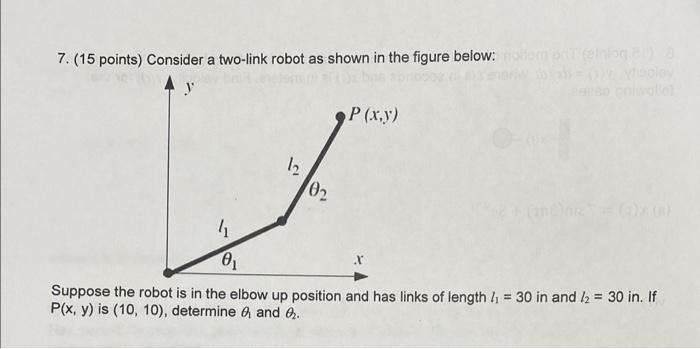
Solved 7 15 Points Consider A Two Link Robot As Shown In Chegg Time to understand the jacobian matrix. columns of the jacobian matrix are associated with joints of the robot. each column in the jacobian matrix represents the effect on end effector velocities due to variation in each joint velocity. Hint: you should model these euler angles as the product of three revolute joints along the x; y; z axes and show that when the second angle is =2 the jacobian loses rank.