Solved Consider The Linear Model Yi Xi I I 1 2 N And 1 2

Solved L Consider The Simple Linear Regression Model Yi A Chegg Capm model the capm model was fit to model the excess returns of exxon mobil (y) as a linear function of the excess returns of the market (x) as represented by the s&p 500 index. Question: 2. consider the linear model yi = β1xi εi , i = 1, 2, · · · , n and ε1, ε2, · · · , εn are i.i.d n (0, σ2 ), σ 2 > 0.

Solved Consider The Following Linear Regression Model Yi Chegg We break down yi into two components, the deterministic (nonrandom) com ponent β1 β2xi and the stochastic (random) component ui. the explanatory vari able is xi and the population parameters we want to estimate are given by intercept β1 and the slope β2. the term ui is the disturbance term. The designation simple indicates that there is only one predictor variable x, and linear means that the model is linear in β0 and β1. the intercept β0 and the slope β1 are unknown constants, and they are both called regression coefficients; 2i’s are random errors. Example 0.2 (r demonstration). consider the dataset that contains weights and heights of 507 physically active individuals (247 men and 260 women).1 we fit a regression line of weight (y) versus height (x) by r. In depth understanding of linear model helps learning further topics. this chapter is slightly more advanced than chapter 3 of consider linear regression model. where yi xi are the i th observation of the response and covariates. here xi is of 1 dimension.

Solved A Linear Regression Model Yi β0 β1xi I I Chegg Example 0.2 (r demonstration). consider the dataset that contains weights and heights of 507 physically active individuals (247 men and 260 women).1 we fit a regression line of weight (y) versus height (x) by r. In depth understanding of linear model helps learning further topics. this chapter is slightly more advanced than chapter 3 of consider linear regression model. where yi xi are the i th observation of the response and covariates. here xi is of 1 dimension. Consider the simple linear regression model y i =β0 β1xi ϵi i=1,2,…,n where the ϵi 's are independent and identically distributed random variables with e(ϵi)= 0 the sum squared error (sse) is given by sse= ∑i=1n (yi−y^i)2 = ∑i=1n (yi−β^0−β^1xi)2 where y^i is the predicted value of y when x=xi. The simple linear regression model specifies that the mean, or expected value of y is a linear function of the level of x. further, x is presumed to be set by the experimenter (as in controlled experiments) or known in advance to the activity generating the response y . However, we do not know the above true model and fit the data points on the simple linear model: e (y ) = β0 β1x, and obtain the least squares estimator for β0 and β1:. Linear regression model in this chapter, we consider the following regression model: yi = f(xi) εi, i = 1, . . . , n , (2.1) where ε = (ε1, . . . , εn)⊤ is sub gaussian with variance proxy σ2 and such that ie[ε] = 0. our goal is to estimate the function f under a linear assumption.
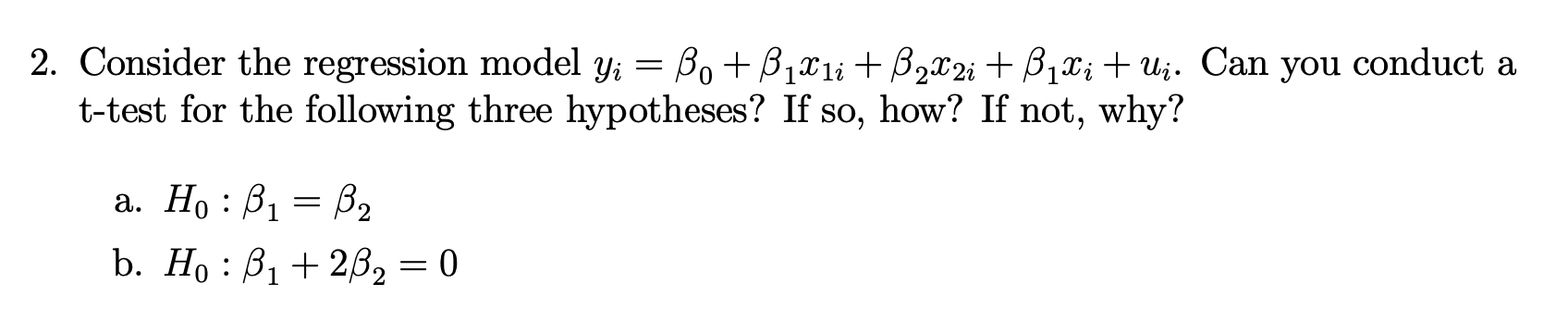
Consider The Regression Model Yi 0 1x1i 2x2i Chegg Consider the simple linear regression model y i =β0 β1xi ϵi i=1,2,…,n where the ϵi 's are independent and identically distributed random variables with e(ϵi)= 0 the sum squared error (sse) is given by sse= ∑i=1n (yi−y^i)2 = ∑i=1n (yi−β^0−β^1xi)2 where y^i is the predicted value of y when x=xi. The simple linear regression model specifies that the mean, or expected value of y is a linear function of the level of x. further, x is presumed to be set by the experimenter (as in controlled experiments) or known in advance to the activity generating the response y . However, we do not know the above true model and fit the data points on the simple linear model: e (y ) = β0 β1x, and obtain the least squares estimator for β0 and β1:. Linear regression model in this chapter, we consider the following regression model: yi = f(xi) εi, i = 1, . . . , n , (2.1) where ε = (ε1, . . . , εn)⊤ is sub gaussian with variance proxy σ2 and such that ie[ε] = 0. our goal is to estimate the function f under a linear assumption.
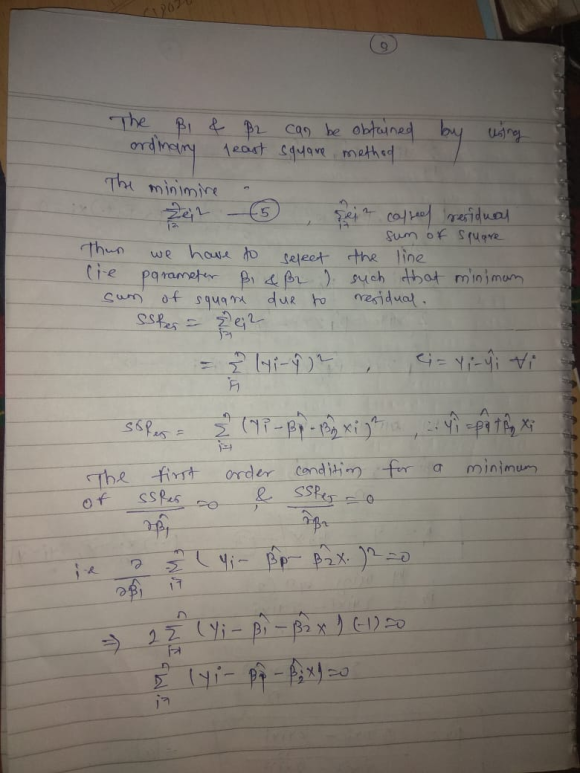
Consider A Simple Linear Model Yi оі1 оі2xi оµi Where оµi в ј N However, we do not know the above true model and fit the data points on the simple linear model: e (y ) = β0 β1x, and obtain the least squares estimator for β0 and β1:. Linear regression model in this chapter, we consider the following regression model: yi = f(xi) εi, i = 1, . . . , n , (2.1) where ε = (ε1, . . . , εn)⊤ is sub gaussian with variance proxy σ2 and such that ie[ε] = 0. our goal is to estimate the function f under a linear assumption.

Solved The Linear Regression Model Is Given Below Yi β0 Chegg
Comments are closed.