Solved Problem Consider A Fir Finite Impulse Response Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. question: consider fir filter defined by the impulse response h [n]=−δ (n) 3δ (n−1)−δ (n−2), what is the frequency response of this filter? a. h (ejω˙)=−1 3e−jω˙−e−j2ω˙ b. Suppose we want to design a digital filter for a signal having bandwidth of 8 khz, and we have to use a 5 pole butterworth filter (commercially available for low cost) for both antialiasing and reconstruction filters.
Solved Consider Fir Filter Defined By The Impulse Response Chegg A finite impulse response (fir) filter is a filter whose impulse response (or response to any finite length input) is of finite duration because it settles to zero in finite time. By choosing the coefficients of the difference equation, the shape of the frequency response vs frequency can be developed. recall that two systems cascaded together, then the overall impulse response is the convolution of the two individual impulse responses. Consider an fir filter whose impulse response is that shown in figure p5–10 (a). given the x ( n ) filter input sequence shown in figure p5–10 (b), draw the filter’s output sequence. Linear phase filters suppose n = 2n 1 is odd and impulse response is symmetric about hn : ht = hn−1−t, t = 0, . . . , n − 1 frequency response.
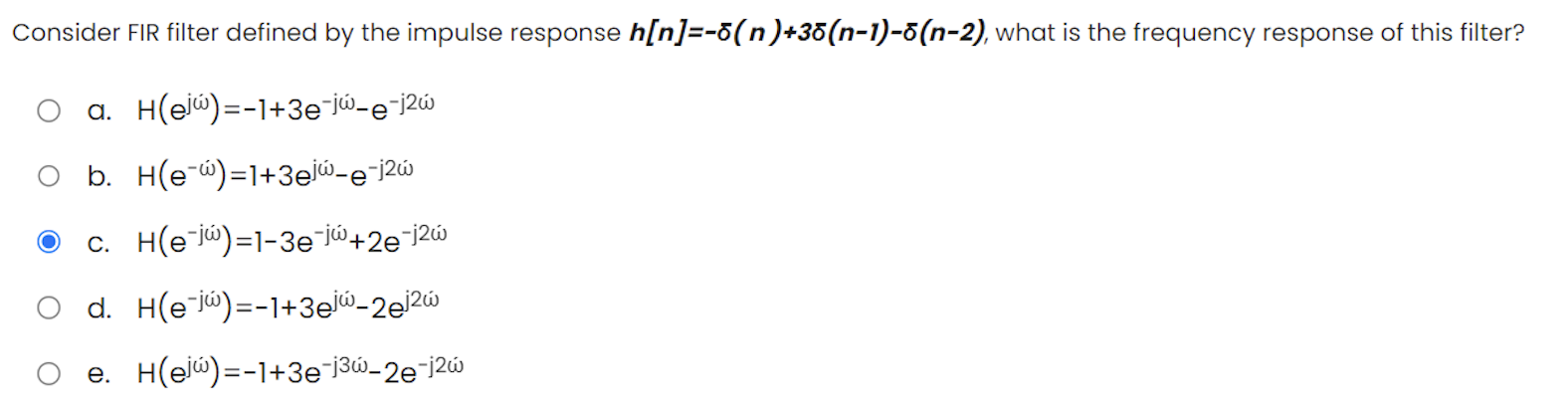
Solved Consider Fir Filter Defined By The Impulse Response Chegg Consider an fir filter whose impulse response is that shown in figure p5–10 (a). given the x ( n ) filter input sequence shown in figure p5–10 (b), draw the filter’s output sequence. Linear phase filters suppose n = 2n 1 is odd and impulse response is symmetric about hn : ht = hn−1−t, t = 0, . . . , n − 1 frequency response. It is interesting to consider the response of the fir and the iir filter to the input shown. in spite of a very simple structure (only 1 delay element, one multiply, and one add) of the recursive filter, it has an excellent low pass function as seen in the output sequence y[n]. We now present a method that approximates the desired frequency response by a linear phase fir amplitude function according to the following optimality criterion. Video answer: consider the fir filter with the impulse response h (n)=\ {1,1,1\}. calculate the magnitude and phase responses and show that the filter has linear phase. There are 2 steps to solve this one. certainly! let's analyze the given fir filter and determine its frequency response. not the question you’re looking for? post any question and get expert help quickly.
Comments are closed.