Solved Complex Puzzles Puzzle 1 Use The Digits 9 To 9 Chegg

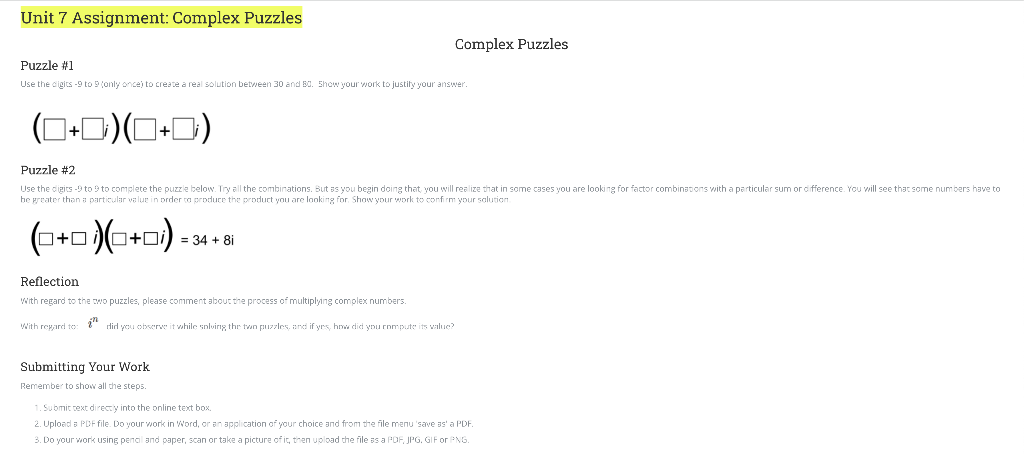
Solved Unit 7 Assignment Complex Puzzles Complex Puzzles Chegg To find a solution for the given equation (a b i) (c d i) that results in a real value between 30 and 80, we need to explore complex puzzles puzzle #1 use the digits 9 to 9 (only once) to create a real solution between 30 and 80. For puzzle #1, we need to find four digits from 9 to 9 (excluding 0) that when multiplied as complex numbers, result in a real number between 30 and 80. we know that the product of two complex conjugates is always a real number.

Solved Complex Puzzles Puzzle 1 Use The Digits 9 To 9 Chegg The process of multiplying these two complex numbers is very similar to multiplying two binomials! multiply each term in the first number by each term in the second number. To solve the first puzzle, use the digits 9 to 9 to create a real solution between 30 and 80 by summing negative and positive digits. the process of multiplying complex numbers involves multiplying the real and imaginary parts separately. Use the digits 9 to 9 to complete the puzzle below. show your work to confirm your solution. Mathematical puzzles are often equations with missing numbers or missing operations that relate to the numbers. at times, the solution to the puzzles is obtained by the hit and trial method.

Solved Complex Puzzles Puzzle 1 Use The Digits 9 To 9 Chegg Use the digits 9 to 9 to complete the puzzle below. show your work to confirm your solution. Mathematical puzzles are often equations with missing numbers or missing operations that relate to the numbers. at times, the solution to the puzzles is obtained by the hit and trial method. Here’s how to approach this question in puzzle #1, start by letting and be the four variables, and put them into the equation using the distributive law of algebra. Unit 7 assignment: complex puzzles directions: puzzle #1 use the digits 9 to 9 (only once) to create a real solution between 30. Click here 👆 to get an answer to your question ️ puzzle #1 use the digits 9 to 9 to create a real solution between 30 and 80. you may only use each digit on. Setting up the problem: we need to find integers a, b, c, and d such that when we multiply two complex numbers (a bi)(c di), we achieve a product of a particular form, possibly in the format p qi where both p and q are known target values derived from sum and their corresponding products.