Solved Calculate The Velocity And Acceleration Vectors Of Chegg

Solved H W 8 Using Vectors For The Same Question That You Chegg Calculate the velocity and acceleration vectors of r (t) = elj – 3 cos (t)k at the time t = 0. (give your answer using component form or standard basis vectors. At this university of colorado boulder website, you can explore the position velocity and acceleration of a ladybug with an interactive simulation that allows you to change these parameters.

Solved Calculate The Velocity And Acceleration Vectors And Chegg Given a position function r (t) that models the position of an object over time, velocity v (t) is the derivative of position, and acceleration a (t) is the derivative of velocity, which means that acceleration is also the second derivative of position. This sequential differentiation reveals the various layers of movement: position, velocity, and acceleration. in physics and engineering, this process is essential for understanding how objects move in space, predicting their future states, and calculating forces acting on them. Step 1 6step 1: calculate the velocity vector by taking the derivative of the position vector with respect to time. in this case, the parameter is $\theta$, so we will take the derivative with respect to $\theta$. To determine the angle between the velocity vector (v) and the acceleration vector (a) at a given time (t = 1.4 sec), we'll first find the expressions for v and a and then calculate the angle between them using the dot product.
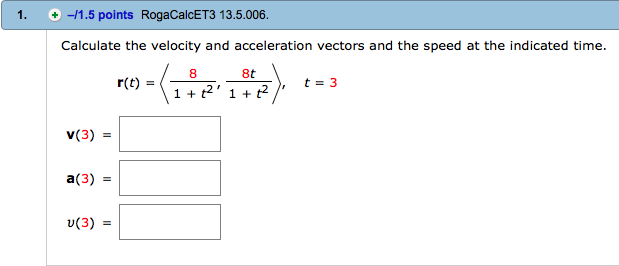
Solved Calculate The Velocity And Acceleration Vectors An Chegg Step 1 6step 1: calculate the velocity vector by taking the derivative of the position vector with respect to time. in this case, the parameter is $\theta$, so we will take the derivative with respect to $\theta$. To determine the angle between the velocity vector (v) and the acceleration vector (a) at a given time (t = 1.4 sec), we'll first find the expressions for v and a and then calculate the angle between them using the dot product. Find the time it takes for the ball to return to the ground. calculate the total distance traveled in the x direction. calculate the velocity vector at the maximum height. determine the acceleration vector at maximum height. Solution: we first calculate the velocity, speed, and acceleration formulas for an arbitrary value of t. in the process, we substitute and find each of these vectors at t = 0. For the velocity of point f, we can apply mehmke's theorem or solve the two vector equations: for the acceleration analysis we use the same points that have been used for the velocity analysis. however we have to write the acceleration of these points in terms of their components. First of all let’s draw the reference frame that we will use to solve the problem. we will also draw the initial conditions. as you can see in the figure above, the positive direction of the axes can be represented in two different ways.
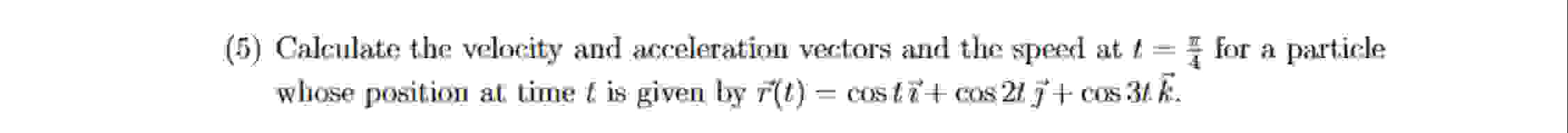
Solved 5 ï Calculate The Velocity And Acceleration Vectors Chegg Find the time it takes for the ball to return to the ground. calculate the total distance traveled in the x direction. calculate the velocity vector at the maximum height. determine the acceleration vector at maximum height. Solution: we first calculate the velocity, speed, and acceleration formulas for an arbitrary value of t. in the process, we substitute and find each of these vectors at t = 0. For the velocity of point f, we can apply mehmke's theorem or solve the two vector equations: for the acceleration analysis we use the same points that have been used for the velocity analysis. however we have to write the acceleration of these points in terms of their components. First of all let’s draw the reference frame that we will use to solve the problem. we will also draw the initial conditions. as you can see in the figure above, the positive direction of the axes can be represented in two different ways.
Comments are closed.