Solved An Fir Filter Is Given By The System Function H Z Chegg

By healtycares On Aug 25, 2025

Solved An Fir Filter Is Given By The System Function H Z Chegg An fir filter is given by the system function h (z) = 1 16 1 16z 4 z 8 determine and draw the direct, linear phase, and cascade form structures. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. One can design a filter with required frequency by placing zeros in the appropriate place. the difference equation of the filter can be obtained by multiplying the factors associated with zeros.

Solved Consider An Fir Filter With System Function Chegg Given each system function h ( z ) for an fir filter given below, specify: the difference equation relating the filter output y [ n ] to the filter input x [n]. Consider an fir filter with system function sketch the direct form and lattice realizations of the filter and determine in detail the corresponding input output equations. To analyze the fir filter given by the system function h (z) = 1 2.88 z 1 3.40 z 2 1.74 z 3 0.4 z 4, identify each coefficient corresponding to the filter's taps for the direct form realization. The system function of a fir filter is given below: h (z)= ∑k=0n −1bkz−k (a) what is the order of this filter? (b) explain the key properties of a linear phase fir filter in terms of the filter coefficients and in terms of the z domain.

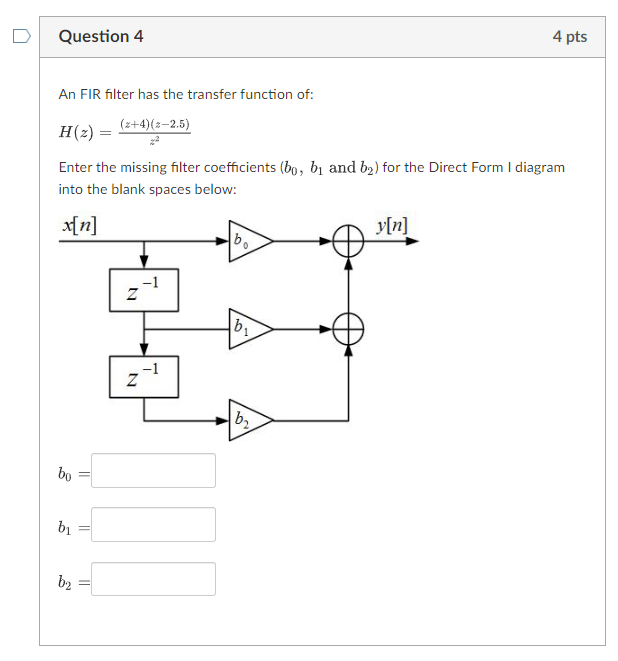
Solved An Fir Filter Has The Transfer Function Of Chegg To analyze the fir filter given by the system function h (z) = 1 2.88 z 1 3.40 z 2 1.74 z 3 0.4 z 4, identify each coefficient corresponding to the filter's taps for the direct form realization. The system function of a fir filter is given below: h (z)= ∑k=0n −1bkz−k (a) what is the order of this filter? (b) explain the key properties of a linear phase fir filter in terms of the filter coefficients and in terms of the z domain. Here’s the best way to solve it. problem 2. a) consider the fir filter with system function: h (z)=(1−z−1)(1−0.5jz−1)(1−0.5z−1) 1. find the difference equation for this filter. 2. find the zeros of this filter. which zeros are on the unit circle? 3. find an expression for the frequency of this filter. Repeat problem 2.1 with an equiripple filter using the "remez" function in matlab. plot the two frequency responses and compare the two filters in terms of performance and complexity. By completing the chapter, students should be able to develop the appropriate filter structure based on the type and characteristics of the fir filter. a difference differential equation, y(n) = x[n] x[n 1]. Our example is for 1st order system with 1 pole only. above statement is true for systems of any order, which can be decomposed into sum of first order systems.

Whether you're here to learn, to share, or simply to indulge in your love for Solved An Fir Filter Is Given By The System Function H Z Chegg, you've found a community that welcomes you with open arms. So go ahead, dive in, and let the exploration begin.

FIR Filters in Cascade: overall transfer function and impulse response

FIR Filters in Cascade: overall transfer function and impulse response

FIR Filters in Cascade: overall transfer function and impulse response Realize the FIR filter whose transfer function is given by 𝐇(𝐳) DSP Lecture 16: FIR filter design using least-squares FIR Filter Design and Software Implementation - Phil's Lab #17 FIR Filter Design DSP | Direct & Cascade realization of the system Realization of FIR Filters | Simple Explanation DSP-fir-filters Realize Linear phase FIR filter for given h(n) Lec 24 DSP slides IIR and FIR Filters, Filter design steps DSP Module 3 Problems on FIR 2 Finding the impulse response given the frequency response of an FIR system Realize the fir filter whose transfer function is given by FIR Filter Lecture- 3c: Design steps Frequency Sampling FIR Filter Design ECE2026 L48: Z-Transforms & Frequency Responses of FIR Filters (Introduction to Signal Processing) DSP - Chapter 7 - FIR Filter Design DSP | 3.2 | FIR filter design with example FIR Filter Design using the Window Method DSP Lectures 16 and 17 - Digital Filters 2; FIR Filter Examples Problem 1: Frequency Characteristics of Window Function in FIR Filter | Discrete Time Signal Process

Conclusion

Upon a thorough analysis, one can see that this particular content delivers beneficial details about Solved An Fir Filter Is Given By The System Function H Z Chegg. All the way through, the journalist displays noteworthy proficiency pertaining to the theme. Crucially, the explanation about important characteristics stands out as especially noteworthy. The author meticulously explains how these factors influence each other to establish a thorough framework of Solved An Fir Filter Is Given By The System Function H Z Chegg.

Further, the piece shines in deciphering complex concepts in an easy-to-understand manner. This comprehensibility makes the analysis useful across different knowledge levels. The analyst further bolsters the analysis by incorporating suitable scenarios and tangible use cases that frame the abstract ideas.

Another aspect that makes this piece exceptional is the exhaustive study of various perspectives related to Solved An Fir Filter Is Given By The System Function H Z Chegg. By exploring these different viewpoints, the publication provides a fair understanding of the matter. The meticulousness with which the writer addresses the topic is genuinely impressive and raises the bar for similar works in this subject.

Wrapping up, this write-up not only educates the viewer about Solved An Fir Filter Is Given By The System Function H Z Chegg, but also encourages deeper analysis into this captivating field. If you are a novice or a seasoned expert, you will encounter worthwhile information in this exhaustive post. Thanks for our article. If you would like to know more, do not hesitate to drop a message through our messaging system. I am excited about your thoughts. For further exploration, you will find several similar pieces of content that you will find interesting and supportive of this topic. Happy reading!