Solved A Very Simple Way To Implement Integer Division Is To Chegg

Solved A Very Simple Way To Implement Integer Division Is To Chegg A very simple way to implement integer division is to repeatedly subtract the divisor (d) from the dividend (n) until the remainder (r) is smaller than the divisor. the number of times you subtract is the quotient (q). There is a faster way to do it if you know the ranges of the values, for example, if you are dividing a signed integer by 3 and you know the range of the value to be divided is 0 to 768, then you can multiply it by a factor and shift it to the left by a power of 2 to that factor divided by 3.

Solved A Very Simple Way To Implement Integer Division Is To Chegg A very simple way to implement integer division is to repeatedly subtract the divisor (d) from the dividend (n) until the remainder (r) is smaller than the divisor. Let's start off with the division algorithm. this says that if you divide an integer a by a positive integer b, you will always get an integer remainder r that is nonnegative, but less than b. Sometimes a problem in number theory can be solved by dividing the integers into various classes depending on their remainders when divided by some number \ (b\). for example, this is helpful in solving the following two problems. A.2 simple divider a very simple way to implement integer division is to repeatedly subtract the divisor (d) from the dividend (n) until the remainder (r) is smaller than the divisor. the number of times you subtract is the quotient (q).

Solved A Very Simple Way To Implement Integer Division Is To Chegg Sometimes a problem in number theory can be solved by dividing the integers into various classes depending on their remainders when divided by some number \ (b\). for example, this is helpful in solving the following two problems. A.2 simple divider a very simple way to implement integer division is to repeatedly subtract the divisor (d) from the dividend (n) until the remainder (r) is smaller than the divisor. the number of times you subtract is the quotient (q). Give an algorithm that combines fractional division and integer division. show the combined implementation, highlighting the modules that are required by the inclusion of integer division. If you say "but i haven't got around to implementing bit wise operators (and, or, shifts, etc.) for my int class yet ", then i say, "do it!". operators like add subtract mult div are all higher order operations, and you first need to do bit wise operators, and build up from there. Implement the unsigned integer division operation using the subtraction method shown in the following activity diagram flowchart. initialize p with 0 times 148 f and d with 0 times 0041. q, r = p d. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. I believe that the answer the author has in mind is something more in the line of binary long division, which can be "efficiently" implemented with shifts, subtractions and comparisons in $o (w)$ steps where $w$ is the machine word length in bits.

Solved 12 11 Lab Simple Integer Division Multiple Chegg Give an algorithm that combines fractional division and integer division. show the combined implementation, highlighting the modules that are required by the inclusion of integer division. If you say "but i haven't got around to implementing bit wise operators (and, or, shifts, etc.) for my int class yet ", then i say, "do it!". operators like add subtract mult div are all higher order operations, and you first need to do bit wise operators, and build up from there. Implement the unsigned integer division operation using the subtraction method shown in the following activity diagram flowchart. initialize p with 0 times 148 f and d with 0 times 0041. q, r = p d. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. I believe that the answer the author has in mind is something more in the line of binary long division, which can be "efficiently" implemented with shifts, subtractions and comparisons in $o (w)$ steps where $w$ is the machine word length in bits.

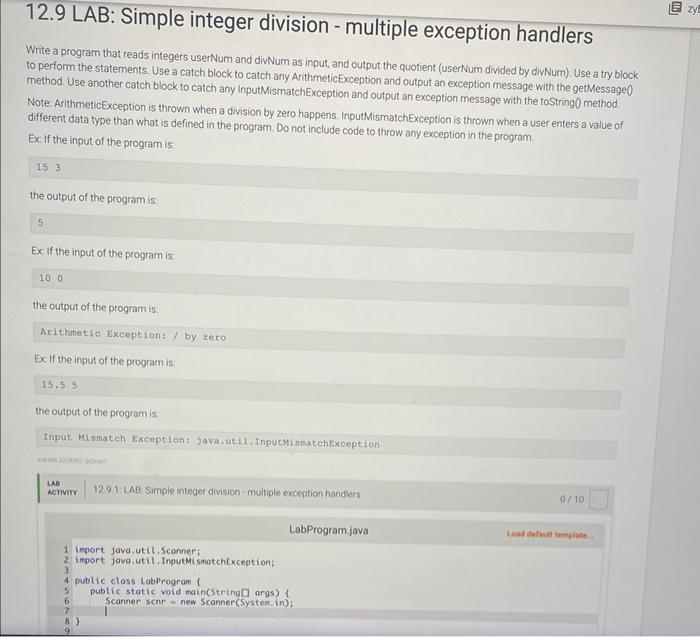
Solved 12 9 Lab Simple Integer Division Multiple Chegg Implement the unsigned integer division operation using the subtraction method shown in the following activity diagram flowchart. initialize p with 0 times 148 f and d with 0 times 0041. q, r = p d. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. I believe that the answer the author has in mind is something more in the line of binary long division, which can be "efficiently" implemented with shifts, subtractions and comparisons in $o (w)$ steps where $w$ is the machine word length in bits.