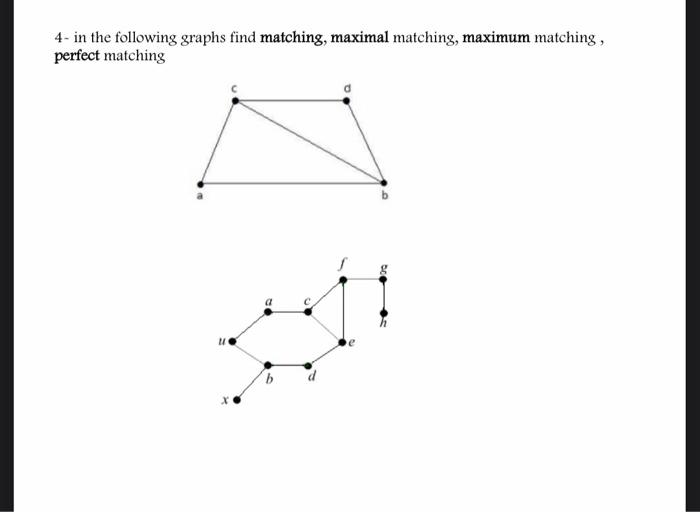
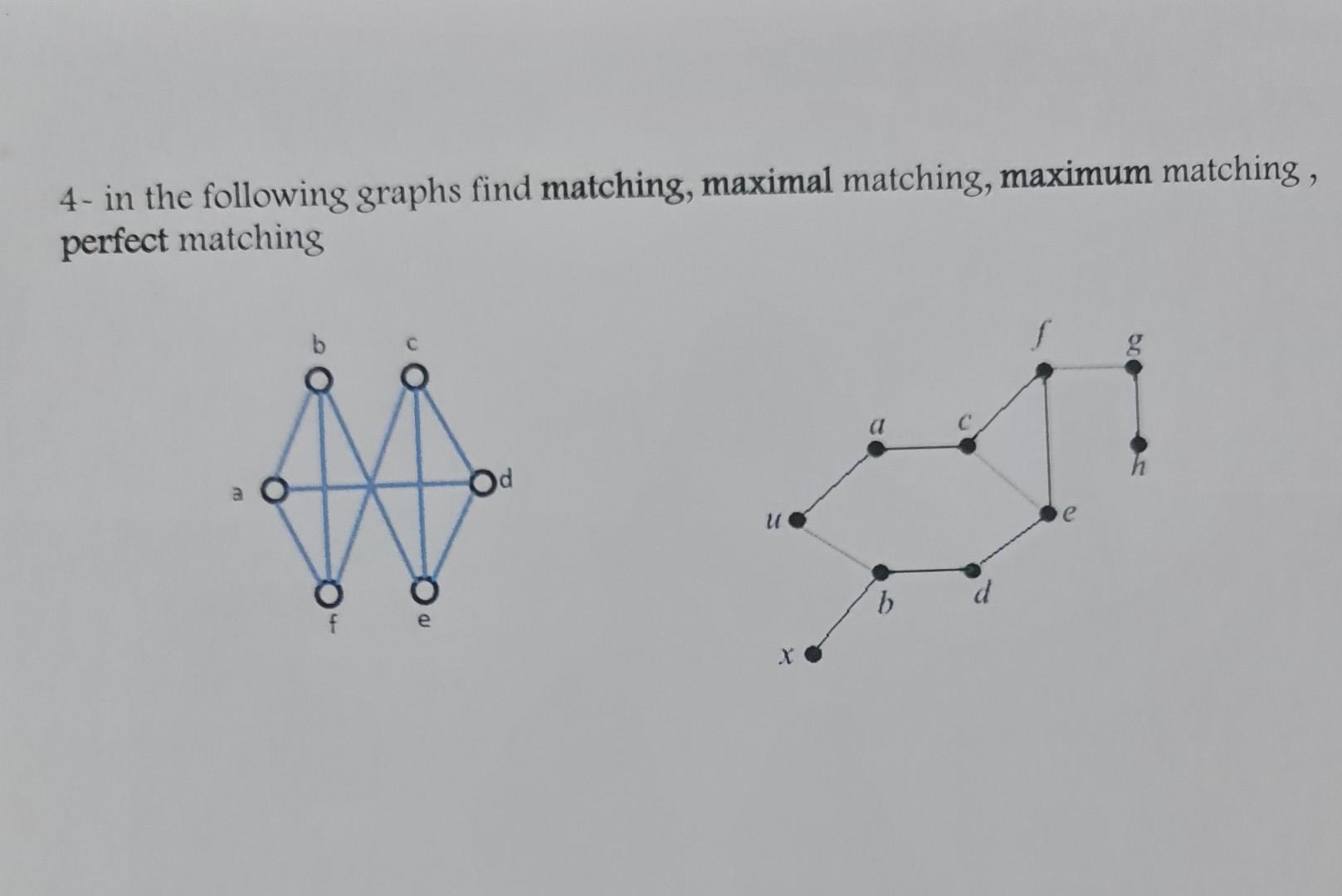
Solved 4 In The Following Graphs Find Matching Maximal Chegg There are 3 steps to solve this one. matching: a matching in a graph is a subset of edges such that no two edges share a common endpoint. not the question you’re looking for? post any question and get expert help quickly. Practice identifying maximal matchings in various graphs to improve your understanding of this concept. 😉 want a more accurate answer? we bring the world's top ai models — our super ai, openai o1, claude 3.5, gpt 4o, gemini 2.0 — together in one place. pick one and see how it solves your question!.
Solved 4 In The Following Graphs Find Matching Maximal Chegg A maximum matching is a matching that contains the largest possible number of edges. a perfect matching is a matching where every vertex is incident to exactly one edge. Consider the graph with four vertices $a,b,c,d$ and three edges $ab,bc,cd$. the matching $\ {ab,cd\}$ with $2$ edges is a maximum matching; in this particular graph there is no matching with more than two edges. Describe the high level steps of a polynomial time algorithm for finding a maximum matching in a graph. describe a polynomial time algorithm that given a bipartite graph and a matching in the graph, determines if an augmenting path exists with respect to the matching. Here’s the best way to solve it. 4: in the following graph, find a maximum matching and a minimum vertex cover. not the question you’re looking for? post any question and get expert help quickly.
Solved 4 In The Following Graphs Find Matching Maximal Chegg Describe the high level steps of a polynomial time algorithm for finding a maximum matching in a graph. describe a polynomial time algorithm that given a bipartite graph and a matching in the graph, determines if an augmenting path exists with respect to the matching. Here’s the best way to solve it. 4: in the following graph, find a maximum matching and a minimum vertex cover. not the question you’re looking for? post any question and get expert help quickly. Find a maximum matching. if possible find a matching which is maximal but not not maximum. either find an x saturating matching or find a set s such that |s| > |n (s)|. (a, c), (b, d) or (a, b), (c, d). all maximal matchings are maximum. | {c, d}| = 2, but |n ( {c, d})| = | {a}| = 1. As a warm up exercise, this section discusses the maximal matching problem. given a graph \ (g = (v, e)\), the problem is to find a matching \ (m \subseteq e\) such that there is no matching \ (m'\) that satisfies \ (m \subset m' \subseteq e\). The time complexity of the above algorithm is o (v*e) where v is the number of vertices in the graph and e is the number of edges. the algorithm iterates over each vertex in the graph and then performs a dfs on the corresponding edges to find the maximum bipartite matching. Consider the following graph: (a) find a maximum matching of the graph; that is, a matching with the most possible edges. (b) use tutte's theorem to show that this graph does not have a perfect matching.
Comments are closed.